!pip list | grep scipyscipy 1.12.0Benedict Thekkel
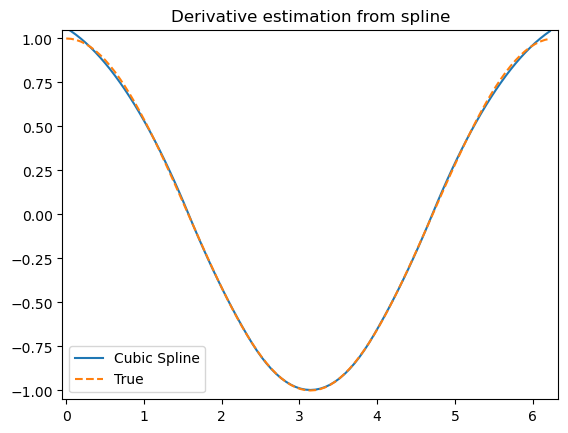
array(5.57083333)import matplotlib.pyplot as plt
fig, ax = plt.subplots(4, 1, figsize=(5, 7))
xnew = np.linspace(0, 10, num=1001)
ax[0].plot(xnew, spl(xnew))
ax[0].plot(x, y, 'o', label='data')
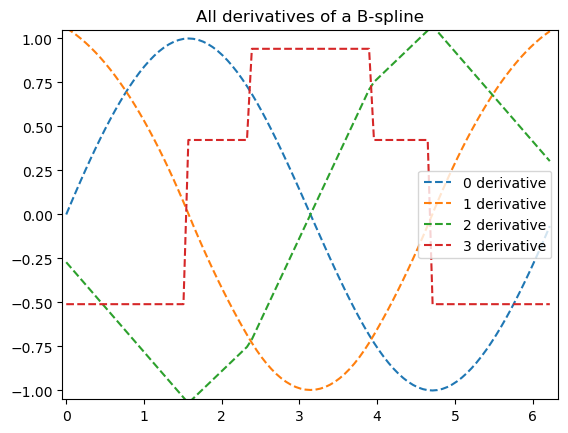
ax[1].plot(xnew, spl(xnew, nu=1), '--', label='1st derivative')
ax[2].plot(xnew, spl(xnew, nu=2), '--', label='2nd derivative')
ax[3].plot(xnew, spl(xnew, nu=3), '--', label='3rd derivative')
for j in range(4):
ax[j].legend(loc='best')
plt.tight_layout()
plt.show()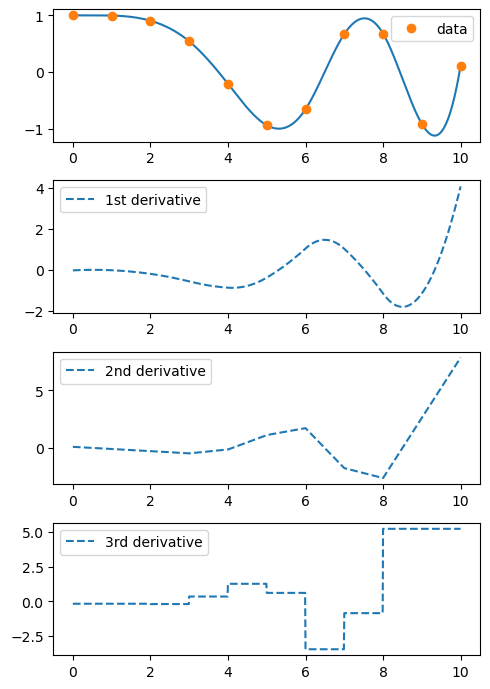
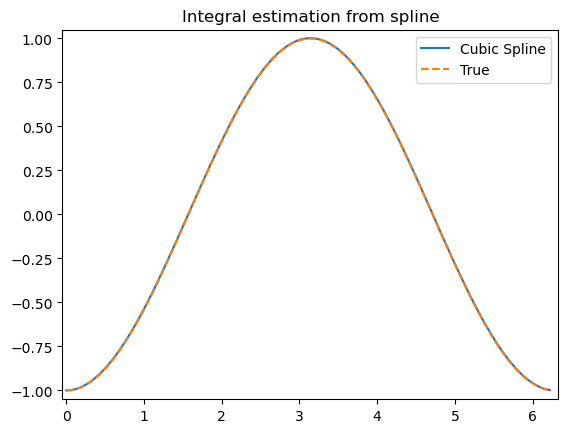
der = bspl.derivative() # a BSpline representing the derivative
import matplotlib.pyplot as plt
xx = np.linspace(0, 3/2, 51)
plt.plot(xx, bspl(xx), '--', label=r'$\sin(\pi x)$ approx')
plt.plot(x, y, 'o', label='data')
plt.plot(xx, der(xx)/np.pi, '--', label='$d \sin(\pi x)/dx / \pi$ approx')
plt.legend()
plt.show()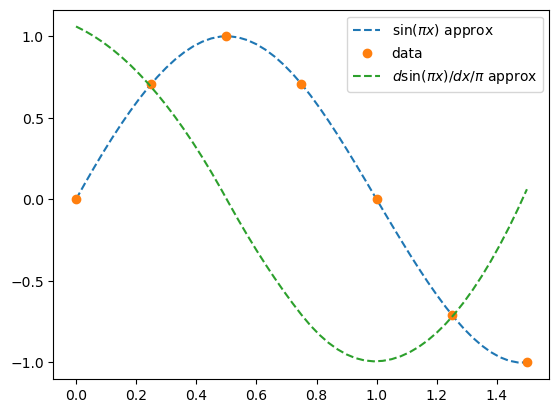
array([[0, 1, 2, 3, 4, 5, 6],
[0, 0, 0, 9, 0, 0, 0]])from scipy.interpolate import make_interp_spline
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 3, figsize=(8, 3))
parametrizations = ['uniform', 'cord length', 'centripetal']
for j, u in enumerate([u_unif, u_cord, u_c]):
spl = make_interp_spline(u, p, axis=1) # note p is a 2D array
uu = np.linspace(u[0], u[-1], 51)
xx, yy = spl(uu)
ax[j].plot(xx, yy, '--')
ax[j].plot(p[0, :], p[1, :], 'o')
ax[j].set_title(parametrizations[j])
plt.show()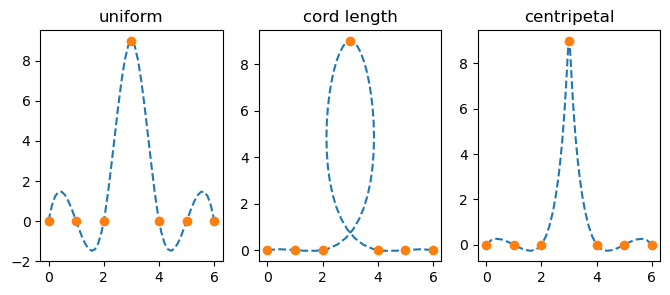
[0. 0. 0. 0. 0.5 0.75 1. 1.5 1.5 1.5 1.5 ]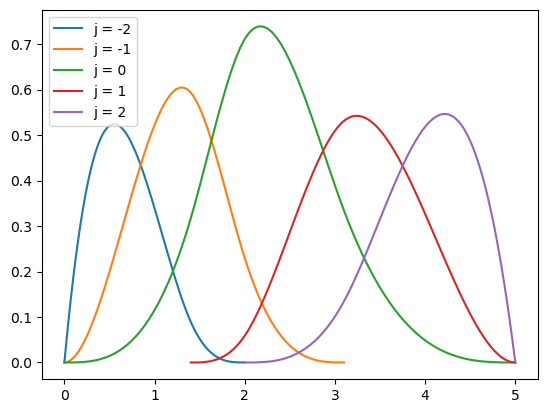
<3x7 sparse array of type '<class 'numpy.float64'>'
with 12 stored elements in Compressed Sparse Row format>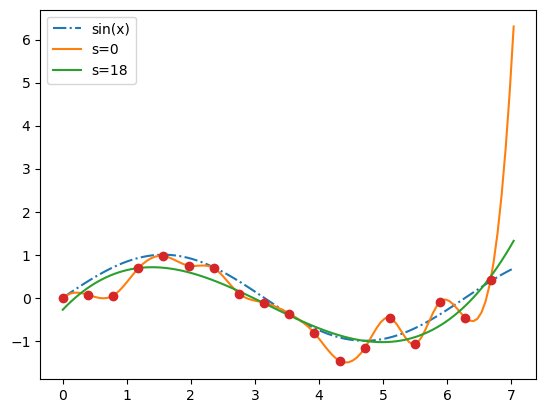
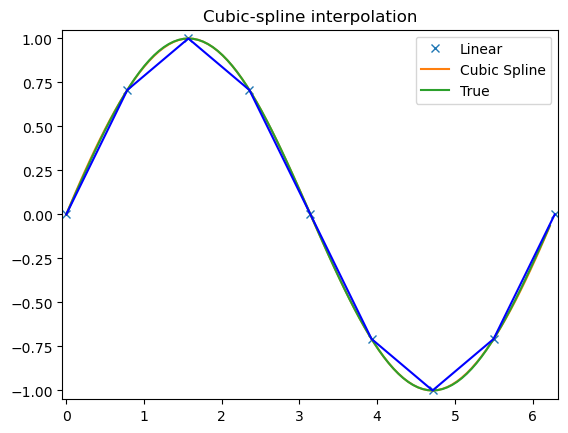
array([-2.22044605e-16, 3.14159265e+00, 6.28318531e+00])t = np.arange(0, 1.1, .1)
x = np.sin(2*np.pi*t)
y = np.cos(2*np.pi*t)
tck, u = interpolate.splprep([x, y], s=0)
unew = np.arange(0, 1.01, 0.01)
out = interpolate.splev(unew, tck)
plt.figure()
plt.plot(x, y, 'x', out[0], out[1], np.sin(2*np.pi*unew), np.cos(2*np.pi*unew), x, y, 'b')
plt.legend(['Linear', 'Cubic Spline', 'True'])
plt.axis([-1.05, 1.05, -1.05, 1.05])
plt.title('Spline of parametrically-defined curve')
plt.show()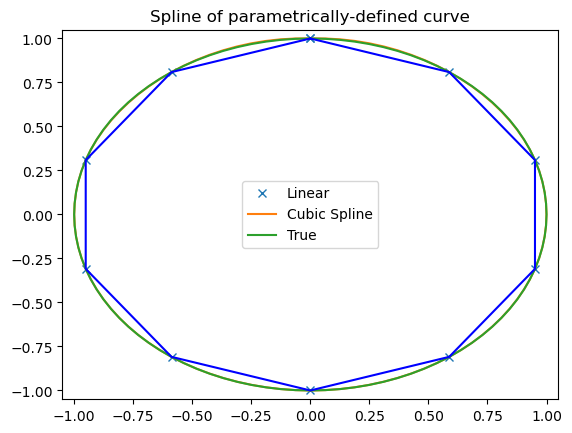
True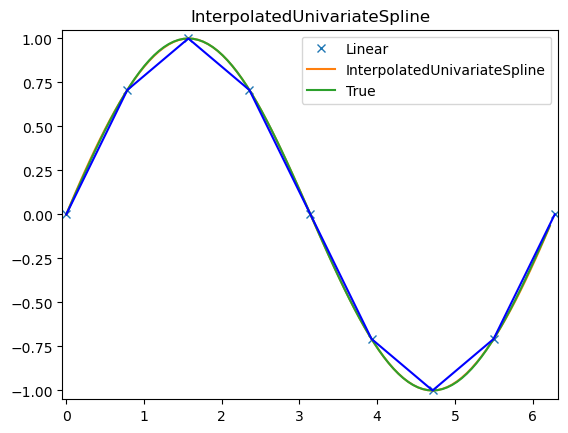
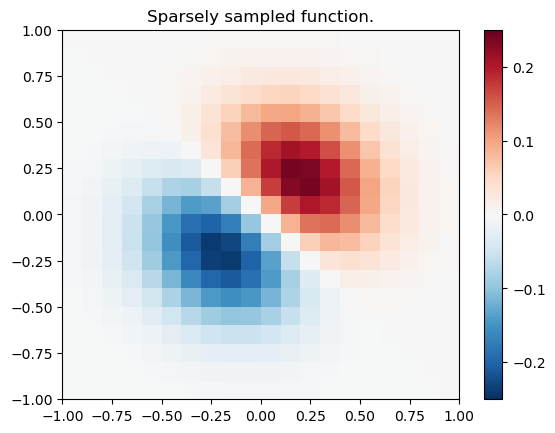
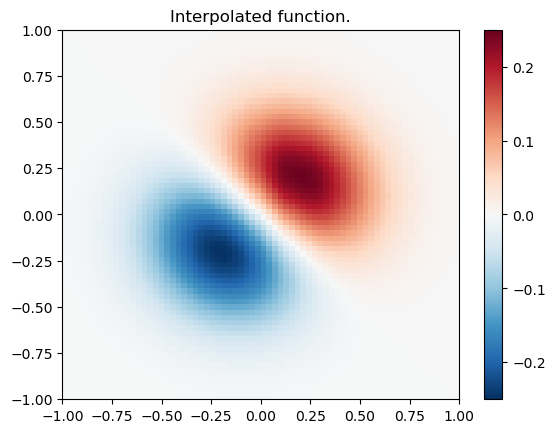
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import SmoothBivariateSpline
import warnings
warnings.simplefilter('ignore')
train_x, train_y = np.meshgrid(np.arange(-5, 5, 0.5), np.arange(-5, 5, 0.5))
train_x = train_x.flatten()
train_y = train_y.flatten()
def z_func(x, y):
return np.cos(x) + np.sin(y) ** 2 + 0.05 * x + 0.1 * y
train_z = z_func(train_x, train_y)
interp_func = SmoothBivariateSpline(train_x, train_y, train_z, s=0.0)
smth_func = SmoothBivariateSpline(train_x, train_y, train_z)
test_x = np.arange(-9, 9, 0.01)
test_y = np.arange(-9, 9, 0.01)
grid_x, grid_y = np.meshgrid(test_x, test_y)
interp_result = interp_func(test_x, test_y).T
smth_result = smth_func(test_x, test_y).T
perfect_result = z_func(grid_x, grid_y)
fig, axes = plt.subplots(1, 3, figsize=(16, 8))
extent = [test_x[0], test_x[-1], test_y[0], test_y[-1]]
opts = dict(aspect='equal', cmap='nipy_spectral', extent=extent, vmin=-1.5, vmax=2.5)
im = axes[0].imshow(perfect_result, **opts)
fig.colorbar(im, ax=axes[0], orientation='horizontal')
axes[0].plot(train_x, train_y, 'w.')
axes[0].set_title('Perfect result, sampled function', fontsize=21)
im = axes[1].imshow(smth_result, **opts)
axes[1].plot(train_x, train_y, 'w.')
fig.colorbar(im, ax=axes[1], orientation='horizontal')
axes[1].set_title('s=default', fontsize=21)
im = axes[2].imshow(interp_result, **opts)
fig.colorbar(im, ax=axes[2], orientation='horizontal')
axes[2].plot(train_x, train_y, 'w.')
axes[2].set_title('s=0', fontsize=21)
plt.tight_layout()
plt.show()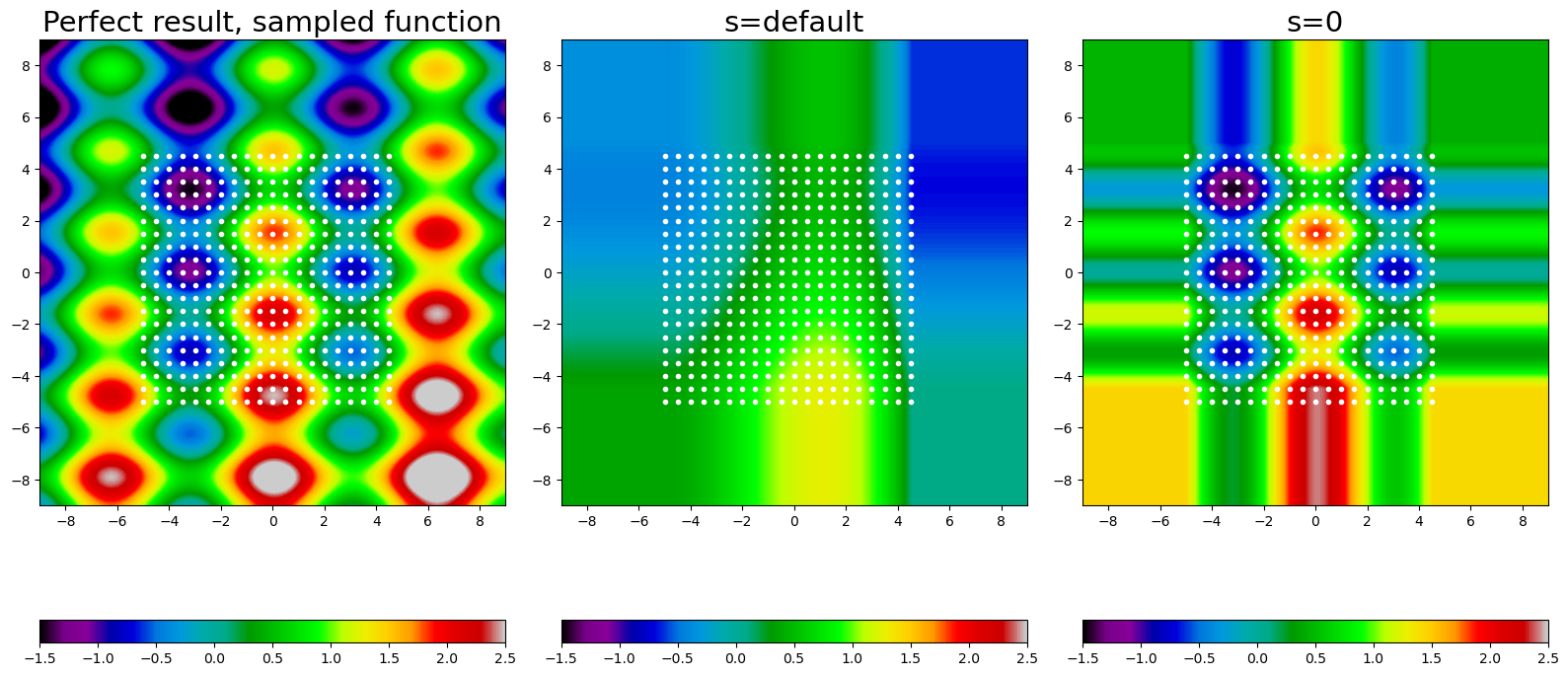
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import RectBivariateSpline
x = np.arange(-5.01, 5.01, 0.25) # the grid is an outer product
y = np.arange(-5.01, 7.51, 0.25) # of x and y arrays
xx, yy = np.meshgrid(x, y, indexing='ij')
z = np.sin(xx**2 + 2.*yy**2) # z array needs to be 2-D
func = RectBivariateSpline(x, y, z, s=0)
xnew = np.arange(-5.01, 5.01, 1e-2)
ynew = np.arange(-5.01, 7.51, 1e-2)
znew = func(xnew, ynew)
plt.imshow(znew)
plt.colorbar()
plt.show()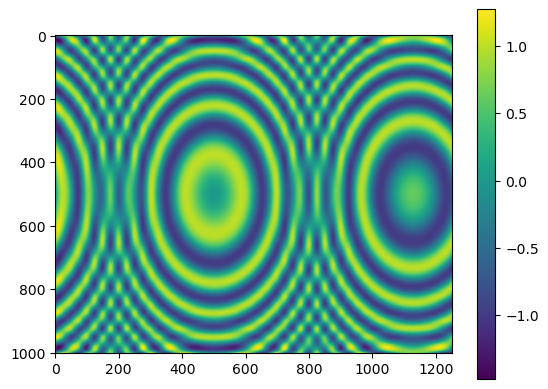
interp = RegularGridInterpolator(fit_points, values)
fig, axes = plt.subplots(2, 3, figsize=(10, 6))
axes = axes.ravel()
fig_index = 0
for method in ['linear', 'nearest', 'slinear', 'cubic', 'quintic']:
im = interp(test_points, method=method).reshape(80, 80)
axes[fig_index].imshow(im)
axes[fig_index].set_title(method)
axes[fig_index].axis("off")
fig_index += 1
axes[fig_index].imshow(true_values)
axes[fig_index].set_title("True values")
fig.tight_layout()
fig.show()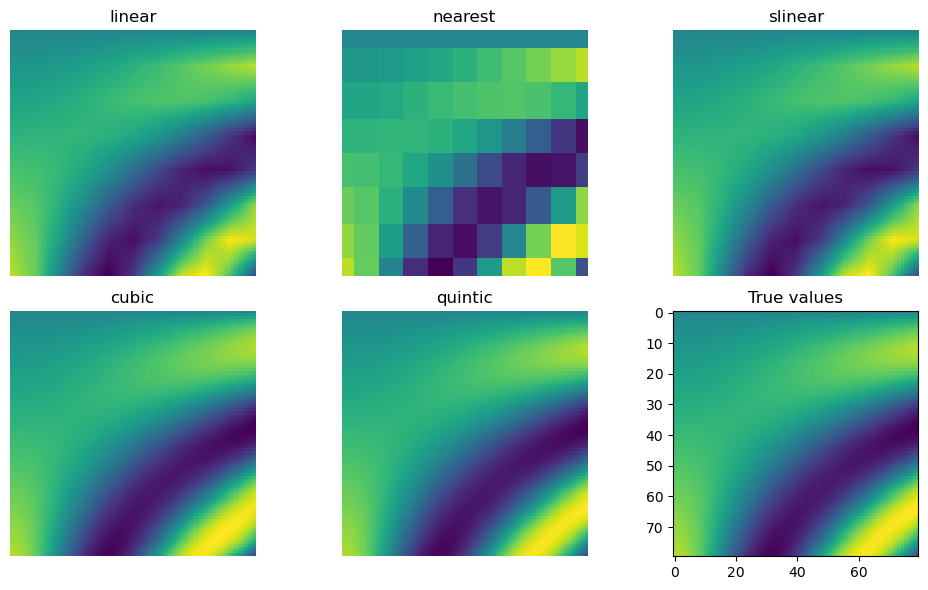
Truearray([2., 2., 2.])class CartesianGridInterpolator:
def __init__(self, points, values, method='linear'):
self.limits = np.array([[min(x), max(x)] for x in points])
self.values = np.asarray(values, dtype=float)
self.order = {'linear': 1, 'cubic': 3, 'quintic': 5}[method]
def __call__(self, xi):
"""
`xi` here is an array-like (an array or a list) of points.
Each "point" is an ndim-dimensional array_like, representing
the coordinates of a point in ndim-dimensional space.
"""
# transpose the xi array into the ``map_coordinates`` convention
# which takes coordinates of a point along columns of a 2D array.
xi = np.asarray(xi).T
# convert from data coordinates to pixel coordinates
ns = self.values.shape
coords = [(n-1)*(val - lo) / (hi - lo)
for val, n, (lo, hi) in zip(xi, ns, self.limits)]
# interpolate
return map_coordinates(self.values, coords,
order=self.order,
cval=np.nan) # fill_valuearray([ 9. , 64.9])import matplotlib.pyplot as plt
plt.subplot(221)
plt.imshow(func(grid_x, grid_y).T, extent=(0, 1, 0, 1), origin='lower')
plt.plot(points[:, 0], points[:, 1], 'k.', ms=1) # data
plt.title('Original')
plt.subplot(222)
plt.imshow(grid_z0.T, extent=(0, 1, 0, 1), origin='lower')
plt.title('Nearest')
plt.subplot(223)
plt.imshow(grid_z1.T, extent=(0, 1, 0, 1), origin='lower')
plt.title('Linear')
plt.subplot(224)
plt.imshow(grid_z2.T, extent=(0, 1, 0, 1), origin='lower')
plt.title('Cubic')
plt.gcf().set_size_inches(6, 6)
plt.show()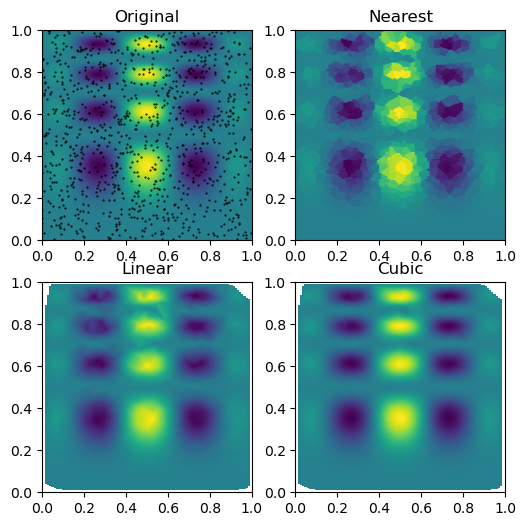
# setup data
x = np.linspace(0, 10, 9).reshape(-1, 1)
y = np.sin(x)
xi = np.linspace(0, 10, 101).reshape(-1, 1)
# use fitpack2 method
ius = InterpolatedUnivariateSpline(x, y)
yi = ius(xi)
plt.subplot(2, 1, 1)
plt.plot(x, y, 'bo')
plt.plot(xi, yi, 'g')
plt.plot(xi, np.sin(xi), 'r')
plt.title('Interpolation using univariate spline')
# use RBF method
rbf = RBFInterpolator(x, y)
fi = rbf(xi)
plt.subplot(2, 1, 2)
plt.plot(x, y, 'bo')
plt.plot(xi, fi, 'g')
plt.plot(xi, np.sin(xi), 'r')
plt.title('Interpolation using RBF - multiquadrics')
plt.show()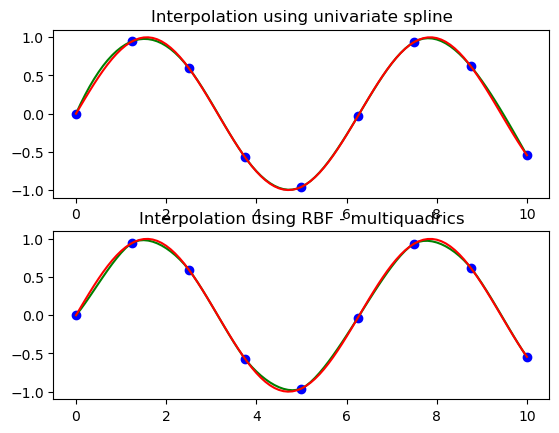
import numpy as np
from scipy.interpolate import RBFInterpolator
import matplotlib.pyplot as plt
# 2-d tests - setup scattered data
rng = np.random.default_rng()
xy = rng.random((100, 2))*4.0-2.0
z = xy[:, 0]*np.exp(-xy[:, 0]**2-xy[:, 1]**2)
edges = np.linspace(-2.0, 2.0, 101)
centers = edges[:-1] + np.diff(edges[:2])[0] / 2.
x_i, y_i = np.meshgrid(centers, centers)
x_i = x_i.reshape(-1, 1)
y_i = y_i.reshape(-1, 1)
xy_i = np.concatenate([x_i, y_i], axis=1)
# use RBF
rbf = RBFInterpolator(xy, z, epsilon=2)
z_i = rbf(xy_i)
# plot the result
fig, ax = plt.subplots()
X_edges, Y_edges = np.meshgrid(edges, edges)
lims = dict(cmap='RdBu_r', vmin=-0.4, vmax=0.4)
mapping = ax.pcolormesh(
X_edges, Y_edges, z_i.reshape(100, 100),
shading='flat', **lims
)
ax.scatter(xy[:, 0], xy[:, 1], 100, z, edgecolor='w', lw=0.1, **lims)
ax.set(
title='RBF interpolation - multiquadrics',
xlim=(-2, 2),
ylim=(-2, 2),
)
fig.colorbar(mapping)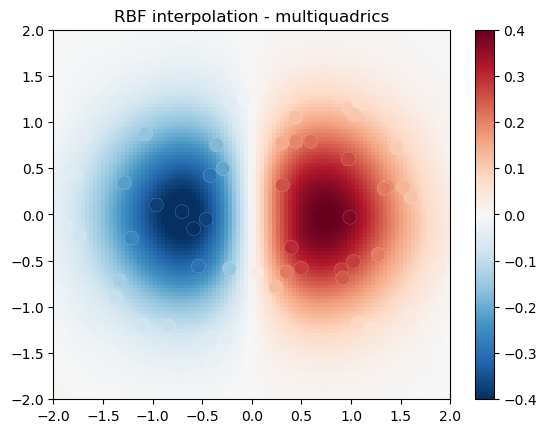
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
x = np.linspace(0, 1.5*np.pi, 11)
y = np.column_stack((np.cos(x), np.sin(x))) # y.shape is (11, 2)
func = interp1d(x, y,
axis=0, # interpolate along columns
bounds_error=False,
kind='linear',
fill_value=(y[0], y[-1]))
xnew = np.linspace(-np.pi, 2.5*np.pi, 51)
ynew = func(xnew)
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
ax1.plot(xnew, ynew[:, 0])
ax1.plot(x, y[:, 0], 'o')
ax2.plot(xnew, ynew[:, 1])
ax2.plot(x, y[:, 1], 'o')
plt.tight_layout()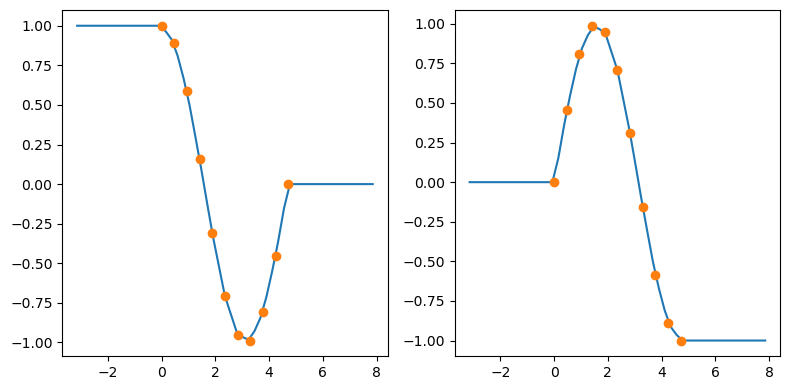
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CubicSpline
xs = [1, 2, 3, 4, 5, 6, 7, 8]
ys = [4.5, 3.6, 1.6, 0.0, -3.3, -3.1, -1.8, -1.7]
notaknot = CubicSpline(xs, ys, bc_type='not-a-knot')
natural = CubicSpline(xs, ys, bc_type='natural')
clamped = CubicSpline(xs, ys, bc_type='clamped')
xnew = np.linspace(min(xs) - 4, max(xs) + 4, 101)
splines = [notaknot, natural, clamped]
titles = ['not-a-knot', 'natural', 'clamped']
fig, axs = plt.subplots(3, 3, figsize=(12, 12))
for i in [0, 1, 2]:
for j, spline, title in zip(range(3), splines, titles):
axs[i, j].plot(xs, spline(xs, nu=i),'o')
axs[i, j].plot(xnew, spline(xnew, nu=i),'-')
axs[i, j].set_title(f'{title}, deriv={i}')
plt.tight_layout()
plt.show()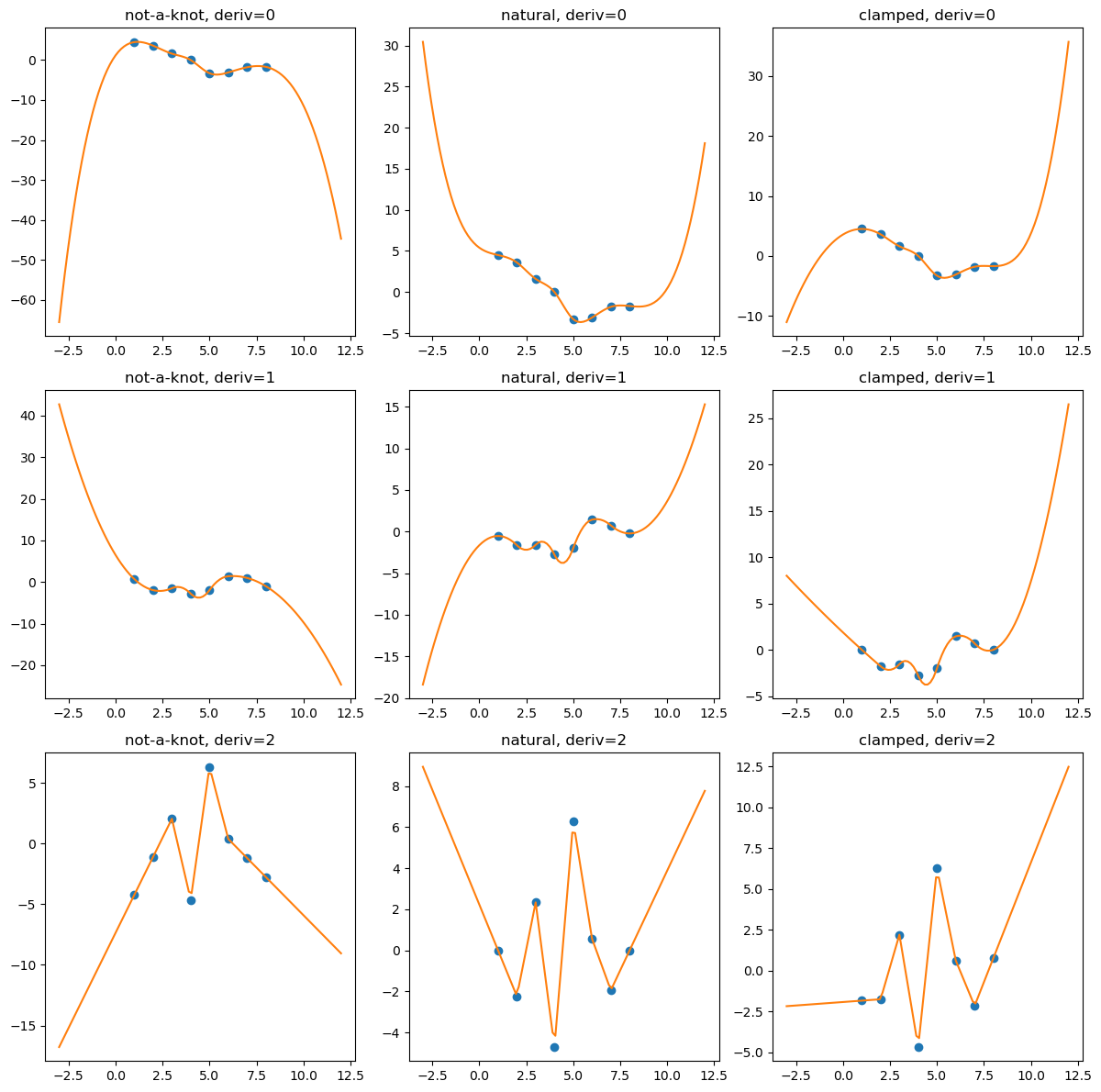
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CubicSpline
def add_boundary_knots(spline):
"""
Add knots infinitesimally to the left and right.
Additional intervals are added to have zero 2nd and 3rd derivatives,
and to maintain the first derivative from whatever boundary condition
was selected. The spline is modified in place.
"""
# determine the slope at the left edge
leftx = spline.x[0]
lefty = spline(leftx)
leftslope = spline(leftx, nu=1)
# add a new breakpoint just to the left and use the
# known slope to construct the PPoly coefficients.
leftxnext = np.nextafter(leftx, leftx - 1)
leftynext = lefty + leftslope*(leftxnext - leftx)
leftcoeffs = np.array([0, 0, leftslope, leftynext])
spline.extend(leftcoeffs[..., None], np.r_[leftxnext])
# repeat with additional knots to the right
rightx = spline.x[-1]
righty = spline(rightx)
rightslope = spline(rightx,nu=1)
rightxnext = np.nextafter(rightx, rightx + 1)
rightynext = righty + rightslope * (rightxnext - rightx)
rightcoeffs = np.array([0, 0, rightslope, rightynext])
spline.extend(rightcoeffs[..., None], np.r_[rightxnext])
xs = [1, 2, 3, 4, 5, 6, 7, 8]
ys = [4.5, 3.6, 1.6, 0.0, -3.3, -3.1, -1.8, -1.7]
notaknot = CubicSpline(xs,ys, bc_type='not-a-knot')
# not-a-knot does not require additional intervals
natural = CubicSpline(xs,ys, bc_type='natural')
# extend the natural natural spline with linear extrapolating knots
add_boundary_knots(natural)
clamped = CubicSpline(xs,ys, bc_type='clamped')
# extend the clamped spline with constant extrapolating knots
add_boundary_knots(clamped)
xnew = np.linspace(min(xs) - 5, max(xs) + 5, 201)
fig, axs = plt.subplots(3, 3,figsize=(12,12))
splines = [notaknot, natural, clamped]
titles = ['not-a-knot', 'natural', 'clamped']
for i in [0, 1, 2]:
for j, spline, title in zip(range(3), splines, titles):
axs[i, j].plot(xs, spline(xs, nu=i),'o')
axs[i, j].plot(xnew, spline(xnew, nu=i),'-')
axs[i, j].set_title(f'{title}, deriv={i}')
plt.tight_layout()
plt.show()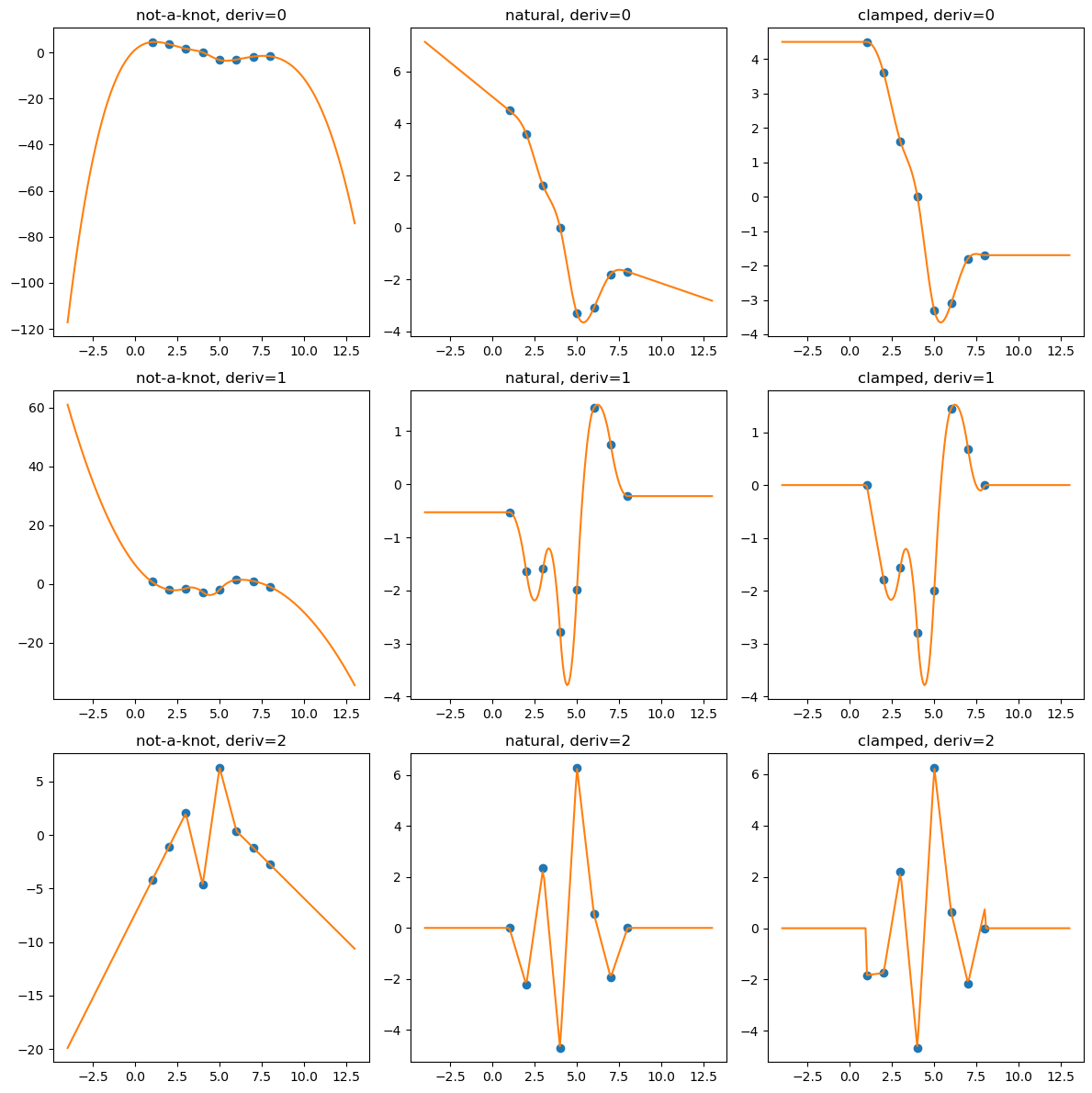
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import brentq
def f(x, a):
return a*x - 1/np.tan(x)
a = 3
x0 = brentq(f, 1e-16, np.pi/2, args=(a,)) # here we shift the left edge
# by a machine epsilon to avoid
# a division by zero at x=0
xx = np.linspace(0.2, np.pi/2, 101)
plt.plot(xx, a*xx, '--')
plt.plot(xx, 1/np.tan(xx), '--')
plt.plot(x0, a*x0, 'o', ms=12)
plt.text(0.1, 0.9, fr'$x_0 = {x0:.3f}$',
transform=plt.gca().transAxes, fontsize=16)
plt.show()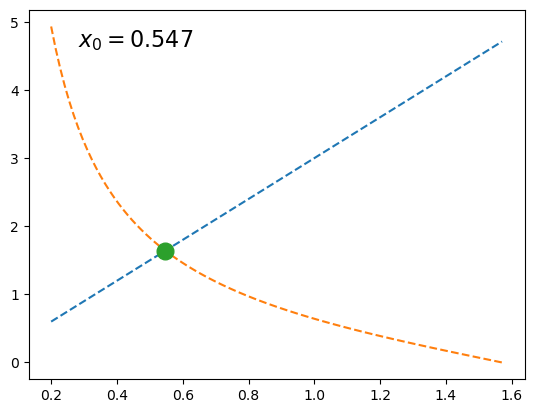
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import BPoly
def f(x, a):
return a*x - 1/np.tan(x)
xleft, xright = 0.2, np.pi/2
x = np.linspace(xleft, xright, 11)
fig, ax = plt.subplots(1, 2, figsize=(12, 4))
for j, a in enumerate([3, 93]):
y = f(x, a)
dydx = a + 1./np.sin(x)**2 # d(ax - 1/tan(x)) / dx
dxdy = 1 / dydx # dx/dy = 1 / (dy/dx)
xdx = np.c_[x, dxdy]
spl = BPoly.from_derivatives(y, xdx) # inverse interpolation
yy = np.linspace(f(xleft, a), f(xright, a), 51)
ax[j].plot(yy, spl(yy), '--')
ax[j].plot(y, x, 'o')
ax[j].set_xlabel(r'$y$')
ax[j].set_ylabel(r'$x$')
ax[j].set_title(rf'$a = {a}$')
ax[j].plot(0, spl(0), 'o', ms=12)
ax[j].text(0.1, 0.85, fr'$x_0 = {spl(0):.3f}$',
transform=ax[j].transAxes, fontsize=18)
ax[j].grid(True)
plt.tight_layout()
plt.show()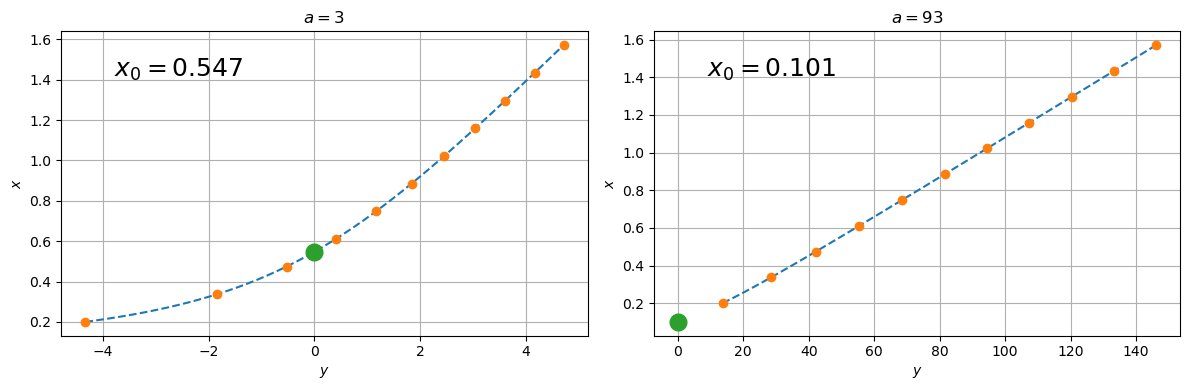
class RootWithAsymptotics:
def __init__(self, a):
# construct the interpolant
xleft, xright = 0.2, np.pi/2
x = np.linspace(xleft, xright, 11)
y = f(x, a)
dydx = a + 1./np.sin(x)**2 # d(ax - 1/tan(x)) / dx
dxdy = 1 / dydx # dx/dy = 1 / (dy/dx)
# inverse interpolation
self.spl = BPoly.from_derivatives(y, np.c_[x, dxdy])
self.a = a
def root(self):
out = self.spl(0)
asympt = 1./np.sqrt(self.a)
return np.where(spl.x.min() < asympt, out, asympt)import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CloughTocher2DInterpolator as CT
def my_CT(xy, z):
"""CT interpolator + nearest-neighbor extrapolation.
Parameters
----------
xy : ndarray, shape (npoints, ndim)
Coordinates of data points
z : ndarray, shape (npoints)
Values at data points
Returns
-------
func : callable
A callable object which mirrors the CT behavior,
with an additional neareast-neighbor extrapolation
outside of the data range.
"""
x = xy[:, 0]
y = xy[:, 1]
f = CT(xy, z)
# this inner function will be returned to a user
def new_f(xx, yy):
# evaluate the CT interpolator. Out-of-bounds values are nan.
zz = f(xx, yy)
nans = np.isnan(zz)
if nans.any():
# for each nan point, find its nearest neighbor
inds = np.argmin(
(x[:, None] - xx[nans])**2 +
(y[:, None] - yy[nans])**2
, axis=0)
# ... and use its value
zz[nans] = z[inds]
return zz
return new_f
# Now illustrate the difference between the original ``CT`` interpolant
# and ``my_CT`` on a small example:
x = np.array([1, 1, 1, 2, 2, 2, 4, 4, 4])
y = np.array([1, 2, 3, 1, 2, 3, 1, 2, 3])
z = np.array([0, 7, 8, 3, 4, 7, 1, 3, 4])
xy = np.c_[x, y]
lut = CT(xy, z)
lut2 = my_CT(xy, z)
X = np.linspace(min(x) - 0.5, max(x) + 0.5, 71)
Y = np.linspace(min(y) - 0.5, max(y) + 0.5, 71)
X, Y = np.meshgrid(X, Y)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_wireframe(X, Y, lut(X, Y), label='CT')
ax.plot_wireframe(X, Y, lut2(X, Y), color='m',
cstride=10, rstride=10, alpha=0.7, label='CT + n.n.')
ax.scatter(x, y, z, 'o', color='k', s=48, label='data')
ax.legend()
plt.tight_layout()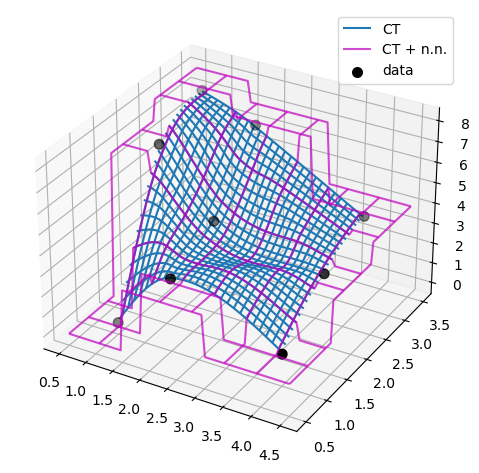
array([ 4.5 -0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j, -1.83155948-1.60822041j,
2.08155948+1.65109876j])from scipy.fft import fft, fftfreq
import numpy as np
# Number of sample points
N = 600
# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N, endpoint=False)
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = fft(y)
xf = fftfreq(N, T)[:N//2]
import matplotlib.pyplot as plt
plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.grid()
plt.show()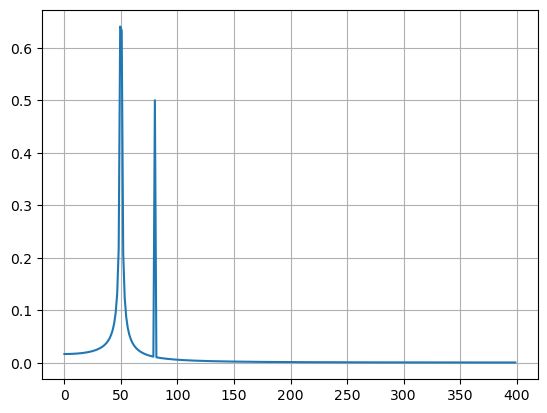
from scipy.fft import fft, fftfreq
import numpy as np
# Number of sample points
N = 600
# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N, endpoint=False)
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = fft(y)
from scipy.signal.windows import blackman
w = blackman(N)
ywf = fft(y*w)
xf = fftfreq(N, T)[:N//2]
import matplotlib.pyplot as plt
plt.semilogy(xf[1:N//2], 2.0/N * np.abs(yf[1:N//2]), '-b')
plt.semilogy(xf[1:N//2], 2.0/N * np.abs(ywf[1:N//2]), '-r')
plt.legend(['FFT', 'FFT w. window'])
plt.grid()
from scipy.fft import fftshift
x = np.arange(8)
fftshift(x)
plt.show()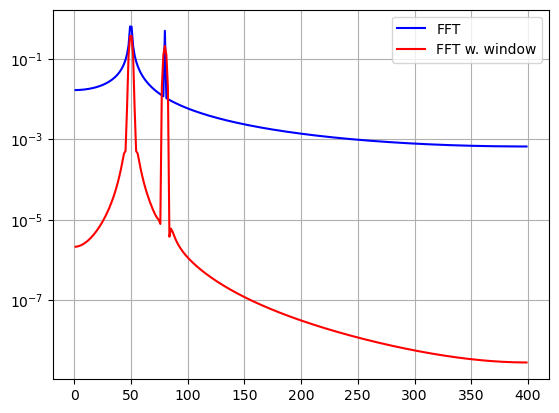
array([ 0., 1., 2., 3., -4., -3., -2., -1.])from scipy.fft import fftshift
x = np.arange(8)
fftshift(x)
from scipy.fft import fft, fftfreq, fftshift
import numpy as np
# number of signal points
N = 400
# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N, endpoint=False)
y = np.exp(50.0 * 1.j * 2.0*np.pi*x) + 0.5*np.exp(-80.0 * 1.j * 2.0*np.pi*x)
yf = fft(y)
xf = fftfreq(N, T)
xf = fftshift(xf)
yplot = fftshift(yf)
import matplotlib.pyplot as plt
plt.plot(xf, 1.0/N * np.abs(yplot))
plt.grid()
plt.show()
array([ 5.5 -0.j , 2.25-0.4330127j , -2.75-1.29903811j,
1.5 -0.j , -2.75+1.29903811j, 2.25+0.4330127j ])array([ 4.5 -0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j, -1.83155948-1.60822041j,
2.08155948+1.65109876j])from scipy.fft import ifftn
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
N = 30
f, ((ax1, ax2, ax3), (ax4, ax5, ax6)) = plt.subplots(2, 3, sharex='col', sharey='row')
xf = np.zeros((N,N))
xf[0, 5] = 1
xf[0, N-5] = 1
Z = ifftn(xf)
ax1.imshow(xf, cmap=cm.Reds)
ax4.imshow(np.real(Z), cmap=cm.gray)
xf = np.zeros((N, N))
xf[5, 0] = 1
xf[N-5, 0] = 1
Z = ifftn(xf)
ax2.imshow(xf, cmap=cm.Reds)
ax5.imshow(np.real(Z), cmap=cm.gray)
xf = np.zeros((N, N))
xf[5, 10] = 1
xf[N-5, N-10] = 1
Z = ifftn(xf)
ax3.imshow(xf, cmap=cm.Reds)
ax6.imshow(np.real(Z), cmap=cm.gray)
plt.show()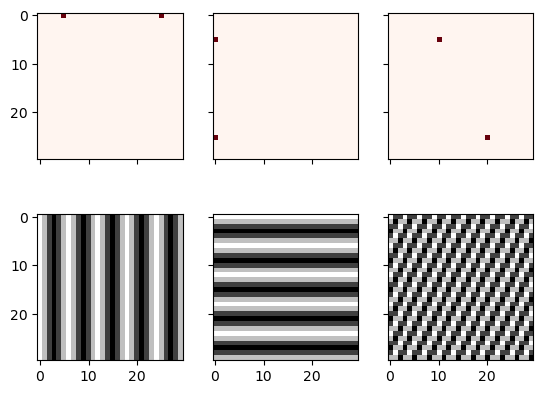
array([ 1. , 2. , 1. , -1. , 1.5])array([ 8., 16., 8., -8., 12.])array([ 1. , 2. , 1. , -1. , 1.5])array([ 10., 20., 10., -10., 15.])array([ 1. , 2. , 1. , -1. , 1.5])0.0009872817275276098array([0., 1., 2., 3., 0., 0., 0.])array([[1., 1., 0., 0., 0., 0., 0.],
[1., 1., 0., 0., 0., 0., 0.],
[0., 0., 1., 1., 0., 0., 0.],
[0., 0., 1., 1., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0.]])array([0.5 , 0.41666667, 0.13888889, 0.0462963 ])(array([1.16666667, 0.63888889, 0.21296296, 0.07098765]), array([0.02366255]))(array([-0.5]), array([0.33333333]), 0.5)import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
b1 = signal.firwin(40, 0.5)
b2 = signal.firwin(41, [0.3, 0.8])
w1, h1 = signal.freqz(b1)
w2, h2 = signal.freqz(b2)
plt.title('Digital filter frequency response')
plt.plot(w1, 20*np.log10(np.abs(h1)), 'b')
plt.plot(w2, 20*np.log10(np.abs(h2)), 'r')
plt.ylabel('Amplitude Response (dB)')
plt.xlabel('Frequency (rad/sample)')
plt.grid()
plt.show()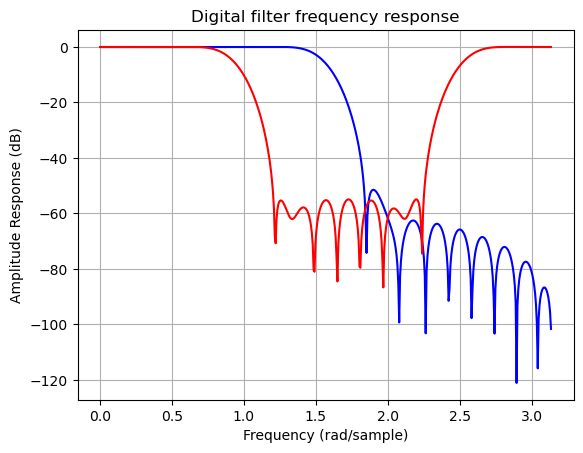
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
b = signal.firwin2(150, [0.0, 0.3, 0.6, 1.0], [1.0, 2.0, 0.5, 0.0])
w, h = signal.freqz(b)
plt.title('Digital filter frequency response')
plt.plot(w, np.abs(h))
plt.title('Digital filter frequency response')
plt.ylabel('Amplitude Response')
plt.xlabel('Frequency (rad/sample)')
plt.grid()
plt.show()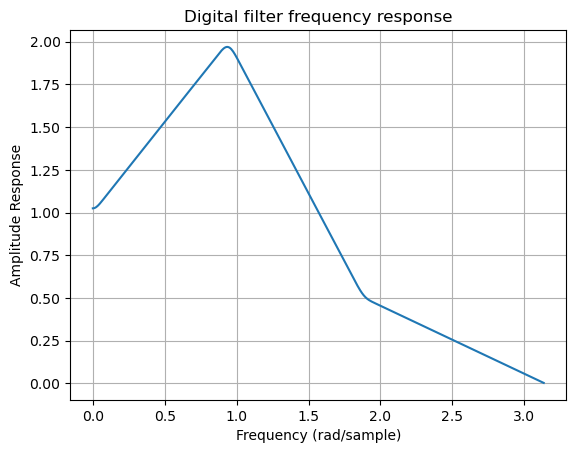
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
b, a = signal.iirfilter(4, Wn=0.2, rp=5, rs=60, btype='lowpass', ftype='ellip')
w, h = signal.freqz(b, a)
plt.title('Digital filter frequency response')
plt.plot(w, 20*np.log10(np.abs(h)))
plt.title('Digital filter frequency response')
plt.ylabel('Amplitude Response [dB]')
plt.xlabel('Frequency (rad/sample)')
plt.grid()
plt.show()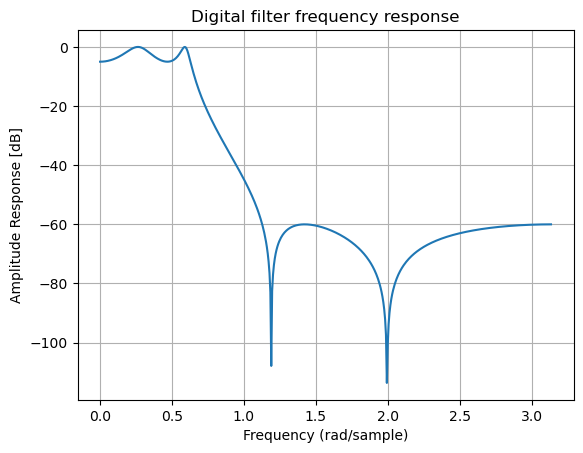
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
b, a = signal.iirdesign(wp=100, ws=200, gpass=2.0, gstop=40., analog=True)
w, h = signal.freqs(b, a)
plt.title('Analog filter frequency response')
plt.plot(w, 20*np.log10(np.abs(h)))
plt.ylabel('Amplitude Response [dB]')
plt.xlabel('Frequency')
plt.grid()
plt.show()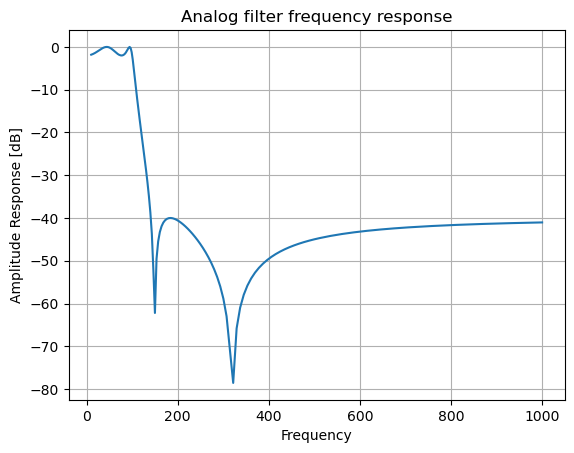
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
fs = 10e3
N = 1e5
amp = 2*np.sqrt(2)
freq = 1270.0
noise_power = 0.001 * fs / 2
time = np.arange(N) / fs
x = amp*np.sin(2*np.pi*freq*time)
x += np.random.normal(scale=np.sqrt(noise_power), size=time.shape)
f, Pper_spec = signal.periodogram(x, fs, 'flattop', scaling='spectrum')
plt.semilogy(f, Pper_spec)
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD')
plt.grid()
plt.show()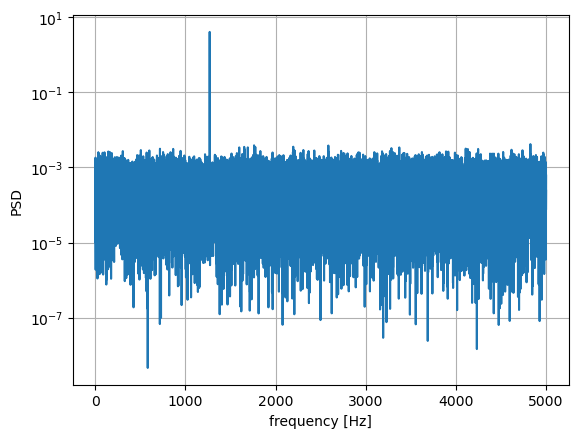
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
fs = 10e3
N = 1e5
amp = 2*np.sqrt(2)
freq = 1270.0
noise_power = 0.001 * fs / 2
time = np.arange(N) / fs
x = amp*np.sin(2*np.pi*freq*time)
x += np.random.normal(scale=np.sqrt(noise_power), size=time.shape)
f, Pwelch_spec = signal.welch(x, fs, scaling='spectrum')
plt.semilogy(f, Pwelch_spec)
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD')
plt.grid()
plt.show()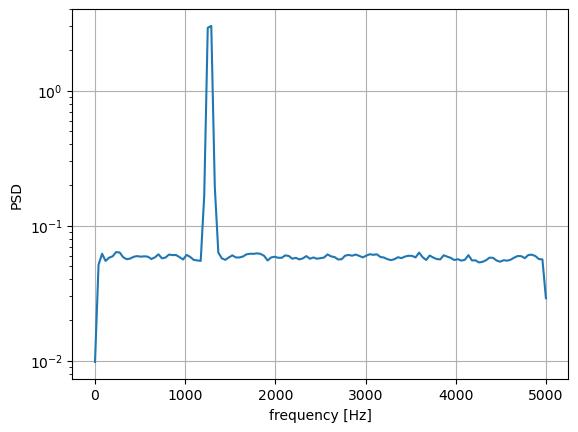
array([ 0, 2, 6, 9, 13, 16, 20, 23, 27, 30])array([[0, 1, 0],
[1, 1, 1],
[0, 1, 0]])array([0, 0, 1, 1, 1, 0, 0])array([ 0, 0, 1, 0, 0, -1, 0])| mode | description | example |
|---|---|---|
| “nearest” | use the value at the boundary | [1 2 3]->[1 1 2 3 3] |
| “wrap” | periodically replicate the array | [1 2 3]->[3 1 2 3 1] |
| “reflect” | reflect the array at the boundary | [1 2 3]->[1 1 2 3 3] |
| “mirror” | mirror the array at the boundary | [1 2 3]->[2 1 2 3 2] |
| “constant” | use a constant value, default is 0.0 | [1 2 3]->[0 1 2 3 0] |
The following synonyms are also supported for consistency with the interpolation routines:
| mode | description |
|---|---|
| “grid-constant” | equivalent to “constant”* |
| “grid-mirror” | equivalent to “reflect” |
| “grid-wrap” | equivalent to “wrap” |
array([[ 0., 0., 0., 0., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 1., -4., 1., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 0., 0., 0., 0.]])array([[ 0., 0., 0., 0., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 1., -4., 1., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 0., 0., 0., 0.]])array([[ 0., 0., 0., 0., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 1., -4., 1., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 0., 0., 0., 0.]])array([[0. , 0. , 0. , 0. , 0. ],
[0. , 1.41421356, 2. , 1.41421356, 0. ],
[0. , 2. , 0. , 2. , 0. ],
[0. , 1.41421356, 2. , 1.41421356, 0. ],
[0. , 0. , 0. , 0. , 0. ]])array([[ 3, 8, 14, 17],
[27, 32, 38, 41],
[51, 56, 62, 65]])array([[ 3, 8, 14, 17],
[27, 32, 38, 41],
[51, 56, 62, 65]])array([[ 3, 8, 14, 17],
[27, 32, 38, 41],
[51, 56, 62, 65]])array([[ 3, 8, 14, 17],
[27, 32, 38, 41],
[51, 56, 62, 65]])array([[ 0, 3, 7, 11],
[12, 15, 19, 23],
[28, 31, 35, 39]])array([[ 0, 3, 7, 11],
[12, 15, 19, 23],
[28, 31, 35, 39]])array([[ 0, 3, 7, 11],
[12, 15, 19, 23],
[28, 31, 35, 39]])array([[ 0, 3, 7, 11],
[12, 15, 19, 23],
[28, 31, 35, 39]])a = np.arange(12).reshape(3,4)
class fnc_class:
def __init__(self, shape):
# store the shape:
self.shape = shape
# initialize the coordinates:
self.coordinates = [0] * len(shape)
def filter(self, buffer):
result = (buffer * np.array([1, 3])).sum()
print(self.coordinates)
# calculate the next coordinates:
axes = list(range(len(self.shape)))
axes.reverse()
for jj in axes:
if self.coordinates[jj] < self.shape[jj] - 1:
self.coordinates[jj] += 1
break
else:
self.coordinates[jj] = 0
return result
fnc = fnc_class(shape = (3,4))
generic_filter(a, fnc.filter, footprint = [[1, 0], [0, 1]])[0, 0]
[0, 1]
[0, 2]
[0, 3]
[1, 0]
[1, 1]
[1, 2]
[1, 3]
[2, 0]
[2, 1]
[2, 2]
[2, 3]array([[ 0, 3, 7, 11],
[12, 15, 19, 23],
[28, 31, 35, 39]])a = np.arange(12).reshape(3,4)
class fnc1d_class:
def __init__(self, shape, axis = -1):
# store the filter axis:
self.axis = axis
# store the shape:
self.shape = shape
# initialize the coordinates:
self.coordinates = [0] * len(shape)
def filter(self, iline, oline):
oline[...] = iline[:-2] + 2 * iline[1:-1] + 3 * iline[2:]
print(self.coordinates)
# calculate the next coordinates:
axes = list(range(len(self.shape)))
# skip the filter axis:
del axes[self.axis]
axes.reverse()
for jj in axes:
if self.coordinates[jj] < self.shape[jj] - 1:
self.coordinates[jj] += 1
break
else:
self.coordinates[jj] = 0
fnc = fnc1d_class(shape = (3,4))
generic_filter1d(a, fnc.filter, 3)[0, 0]
[1, 0]
[2, 0]array([[ 3, 8, 14, 17],
[27, 32, 38, 41],
[51, 56, 62, 65]])array([[0. , 0. , 0. ],
[0. , 1.3625, 2.7375],
[0. , 4.8125, 6.1875],
[0. , 8.2625, 9.6375]])array([[0. , 0. , 0. ],
[0. , 1.3625, 2.7375],
[0. , 4.8125, 6.1875],
[0. , 8.2625, 9.6375]])array([[0. , 0. , 0. ],
[0. , 1.3625, 2.7375],
[0. , 4.8125, 6.1875],
[0. , 8.2625, 9.6375]])array([[ 0., 1., 2.],
[ 3., 4., 5.],
[ 6., 7., 8.],
[ 9., 10., 11.]])array([[False, True, False],
[ True, True, True],
[False, True, False]])array([[ True, True, True],
[ True, True, True],
[ True, True, True]])array([[1, 0, 0, 0, 0],
[1, 1, 0, 1, 0],
[0, 0, 1, 1, 0],
[0, 0, 0, 0, 0]])array([[ True, False, False, False, False],
[ True, True, False, False, False],
[False, False, False, False, False],
[False, False, False, False, False]])array([[False, True, False],
[ True, True, True],
[False, True, False]])array([[0, 1, 1, 0, 0, 0],
[0, 1, 1, 0, 1, 0],
[0, 0, 0, 1, 1, 1],
[0, 0, 0, 0, 1, 0]])(array([[0, 1, 1, 0, 0, 0],
[0, 1, 1, 0, 2, 0],
[0, 0, 0, 2, 2, 2],
[0, 0, 0, 0, 2, 0]], dtype=int32),
2)array([[0, 1, 1, 0, 0, 0],
[0, 1, 1, 0, 1, 0],
[0, 0, 0, 1, 1, 1],
[0, 0, 0, 0, 1, 0]], dtype=int32)input = np.array([[0, 0, 0, 0, 0, 0, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 1, 0, 0, 0, 1, 0],
[0, 1, 0, 0, 0, 1, 0],
[0, 1, 0, 0, 0, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 0, 0, 0, 0, 0]], np.uint8)
markers = np.array([[1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 2, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]], np.int8)
from scipy.ndimage import watershed_ift
watershed_ift(input, markers)array([[1, 1, 1, 1, 1, 1, 1],
[1, 1, 2, 2, 2, 1, 1],
[1, 2, 2, 2, 2, 2, 1],
[1, 2, 2, 2, 2, 2, 1],
[1, 2, 2, 2, 2, 2, 1],
[1, 1, 2, 2, 2, 1, 1],
[1, 1, 1, 1, 1, 1, 1]], dtype=int8)array([[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 2, 2, 2, 1, 1],
[1, 1, 2, 2, 2, 1, 1],
[1, 1, 2, 2, 2, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1]], dtype=int8)array([[-1, -1, -1, -1, -1, -1, -1],
[-1, -1, 2, 2, 2, -1, -1],
[-1, 2, 2, 2, 2, 2, -1],
[-1, 2, 2, 2, 2, 2, -1],
[-1, 2, 2, 2, 2, 2, -1],
[-1, -1, 2, 2, 2, -1, -1],
[-1, -1, -1, -1, -1, -1, -1]], dtype=int8)array([[1, 1],
[1, 1]])[(slice(0, 1, None),), None, (slice(2, 3, None),)]