import torchMatrix and tensor
Matrix and tensor
Initial Checks
torch.cuda.is_available()TrueMatrix multiplication from foundations
from pathlib import Path
import pickle, gzip, math, os, time, shutil, matplotlib as mpl, matplotlib.pyplot as pltGet data
MNIST_URL = 'https://github.com/mnielsen/neural-networks-and-deep-learning/blob/master/data/mnist.pkl.gz?raw=true'
path_data = Path('Data')
path_data.mkdir(exist_ok = True)
path_gz = path_data/'mnist.pkl.gz'path_gzPosixPath('Data/mnist.pkl.gz')from urllib.request import urlretrieve
if not path_gz.exists(): urlretrieve(MNIST_URL, path_gz)with gzip.open(path_gz, 'rb') as f: ((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding = 'latin-1')lst1 = list(x_train[0])
vals = lst1[200:210]
vals[0.0,
0.0,
0.0,
0.19140625,
0.9296875,
0.98828125,
0.98828125,
0.98828125,
0.98828125,
0.98828125]def chunks(x, sz):
for i in range(0, len(x), sz):
yield x[i:i+sz]list(chunks(vals, 5))[[0.0, 0.0, 0.0, 0.19140625, 0.9296875],
[0.98828125, 0.98828125, 0.98828125, 0.98828125, 0.98828125]]mpl.rcParams['image.cmap'] = 'gray'
plt.imshow(list(chunks(lst1, 28)));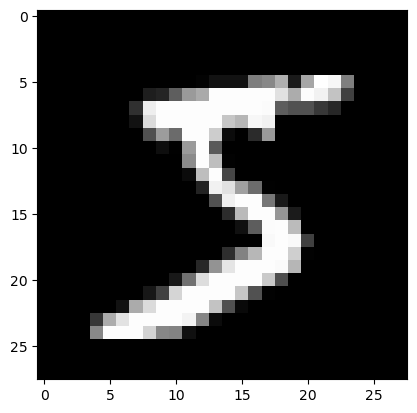
from itertools import isliceit = iter(vals)
islice(it, 5)<itertools.islice>next(it)0.0isit = islice(it,5)next(isit)0.0list(islice(it, 5))[0.0, 0.19140625, 0.9296875, 0.98828125, 0.98828125]it= iter(lst1)
img = list(iter(lambda: list(islice(it,28)), []))plt.imshow(img);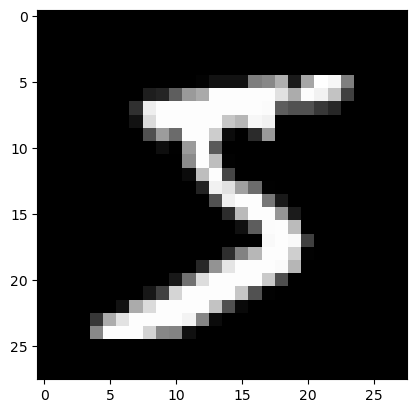
Matrix and tensor
img[20][15]0.98828125class Matrix:
def __init__(self, xs):
self.xs = xs
def __getitem__(self, idxs):
return self.xs[idxs[0]][idxs[1]]m = Matrix(img)
m[20, 15]0.98828125import torch
from torch import tensortensor([1,2,3])tensor([1, 2, 3])tens = tensor(img)
tens[20,15]tensor(0.9883)x_train, y_train, x_valid, y_valid = map(tensor, (x_train, y_train, x_valid, y_valid))
x_train.shapetorch.Size([50000, 784])x_valid.shapetorch.Size([10000, 784])x_train.type()'torch.FloatTensor'imgs = x_train.reshape((-1, 28, 28))
imgs.shapetorch.Size([50000, 28, 28])plt.imshow(imgs[0])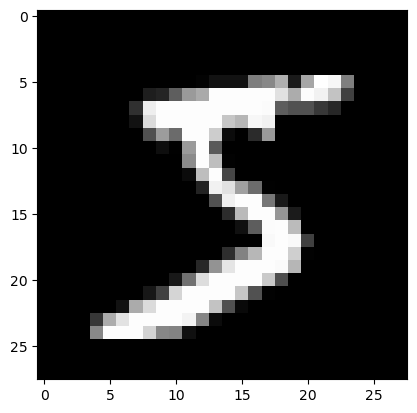
imgs[0, 20, 15]tensor(0.9883)x_train.shapetorch.Size([50000, 784])n,c = x_train.shape
y_train, y_train.shape(tensor([5, 0, 4, ..., 8, 4, 8]), torch.Size([50000]))min(y_train), max(y_train)(tensor(0), tensor(9))y_train.min(), y_train.max()(tensor(0), tensor(9))Random Numbers
Based on the Wichmann Hill Algorithm used before Python 2.3
rnd_state = None
def seed(a):
global rnd_state
a, x = divmod(a, 30268)
a, y = divmod(a, 30306)
a, z = divmod(a, 30322)
rnd_state = int(x)+1, int(y)+1, int(z)+1seed(457428938475)
rnd_state(4976, 20238, 499)def rand():
global rnd_state
x, y, z = rnd_state
x = (171 * x) % 30269
y = (172 * y) % 30307
z = (170 * z) % 30323
rnd_state = x,y,z
return (x/30269 + y/30307 + z/30323) % 1.0rand(),rand(),rand()(0.7645251082582081, 0.7920889799553945, 0.06912886811267205)if os.fork(): print(f'In parent: {rand()}')
else:
print(f'In child: {rand()}')
os._exit(os.EX_OK)In parent: 0.9559050644103264
In child: 0.9559050644103264if os.fork(): print(f'In parent: {torch.rand(1)}')
else:
print(f'In child: {torch.rand(1)}')
os._exit(os.EX_OK)In parent: tensor([0.0657])
In child: tensor([0.0657])plt.plot([rand() for _ in range(50)]);
plt.hist([rand() for _ in range(10000)]);
2.54 ms ± 20.7 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)39.9 µs ± 4.94 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)Matrix Multiplication
torch.manual_seed(1)
weights = torch.randn(784,10)
bias = torch.zeros(10)m1 = x_valid[:5]
m2 = weightsm1.shape, m2.shape(torch.Size([5, 784]), torch.Size([784, 10]))ar, ac = m1.shape
br, bc = m2.shape
(ar,ac),(br,bc)((5, 784), (784, 10))t1 = torch.zeros(ar, bc)
t1.shapetorch.Size([5, 10])for i in range(ar):
for j in range(bc):
for k in range(ac):
t1[i,j] += m1[i,k] * m2 [k, j]t1tensor([[-10.9417, -0.6844, -7.0038, -4.0066, -2.0857, -3.3588, 3.9127,
-3.4375, -11.4696, -2.1153],
[ 14.5430, 5.9977, 2.8914, -4.0777, 6.5914, -14.7383, -9.2787,
2.1577, -15.2772, -2.6758],
[ 2.2204, -3.2171, -4.7988, -6.0453, 14.1661, -8.9824, -4.7922,
-5.4446, -20.6758, 13.5657],
[ -6.7097, 8.8998, -7.4611, -7.8966, 2.6994, -4.7260, -11.0278,
-12.9776, -6.4443, 3.6376],
[ -2.4444, -6.4034, -2.3984, -9.0371, 11.1772, -5.7724, -8.9214,
-3.7862, -8.9827, 5.2797]])t1.shapetorch.Size([5, 10])torch.set_printoptions(precision = 2, linewidth = 140, sci_mode = False)import numpy as np
np.set_printoptions(precision = 2, linewidth = 140)def matmul(a, b):
ar, ac = a.shape
br, bc = b.shape
(ar,ac),(br,bc)
t1 = torch.zeros(ar, bc)
t1.shape
for i in range(ar): #5
for j in range(bc): #10
for k in range(ac): #784
t1[i,j] += m1[i,k] * m2 [k, j]
return t1653 ms ± 10.8 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)ar * bc * ac39200Numba
from numba import njit@njit
def dot(a,b):
res = 0.
for i in range(len(a)): res+=a[i]*b[i]
return resfrom numpy import arrayCPU times: user 404 ms, sys: 79.7 ms, total: 484 ms
Wall time: 757 ms20.01.24 µs ± 111 ns per loop (mean ± std. dev. of 7 runs, 50 loops each)def matmul(a, b):
(ar,ac),(br,bc) = a.shape, b.shape
t1 = torch.zeros(ar, bc)
t1.shape
for i in range(ar): #5
for j in range(bc):
t1[i,j] = dot(a[i,:], b[:, j])
#for k in range(ac): #784
# t1[i,j] += m1[i,k] * m2 [k, j]
return t1m1a, m2a = m1.numpy(), m2.numpy()from fastcore.test import *test_close(t1, matmul(m1a, m2a))381 µs ± 6.52 µs per loop (mean ± std. dev. of 7 runs, 50 loops each)a = [10 ,6 ,4]
b = [2, 8, 7]
a1 = np.array(a)
b1 = np.array(b)
a1 + b1array([12, 14, 11])a2 = tensor(a)
b2 = tensor(b)
a2 + b2tensor([12, 14, 11])(a2 < b2).float().mean()tensor(0.67)m = tensor([[1,2,3],[4,5,6],[7,8,9]])
mtensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])\[\| A \|_F = \left( \sum_{i,j=1}^n | a_{ij} |^2 \right)^{1/2}\]
sf = (m*m).sum()
sftensor(285)sf.sqrt()tensor(16.88)m[2, :], m[:,2](tensor([7, 8, 9]), tensor([3, 6, 9]))m[2]tensor([7, 8, 9])def matmul(a, b):
(ar,ac),(br,bc) = a.shape, b.shape
t1 = torch.zeros(ar, bc)
for i in range(ar): #5
for j in range(bc):
t1[i,j] = (a[i,:] * b[:, j]).sum()
return t1test_close(t1, matmul(m1, m2))1.02 ms ± 16.6 µs per loop (mean ± std. dev. of 7 runs, 50 loops each)def matmul(a, b):
(ar,ac),(br,bc) = a.shape, b.shape
t1 = torch.zeros(ar, bc)
for i in range(ar): #5
for j in range(bc):
t1[i,j] = torch.dot(a[i,:], b[:, j])
return t1test_close(t1, matmul(m1, m2))793 µs ± 8.07 µs per loop (mean ± std. dev. of 7 runs, 50 loops each)Broadcasting with a scalar
a2tensor([10, 6, 4])a2 > 0tensor([True, True, True])a2 + 1tensor([11, 7, 5])mtensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])a2tensor([10, 6, 4])Broadcasting a vector to a matrix
c = tensor([10.,20, 30]);ctensor([10., 20., 30.])mtensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])m.shape, c.shape(torch.Size([3, 3]), torch.Size([3]))c+ mtensor([[11., 22., 33.],
[14., 25., 36.],
[17., 28., 39.]])t = c.expand_as(m)ttensor([[10., 20., 30.],
[10., 20., 30.],
[10., 20., 30.]])t.untyped_storage() 0
0
32
65
0
0
160
65
0
0
240
65
[torch.storage.UntypedStorage(device=cpu) of size 12]t.stride(), t.shape((0, 1), torch.Size([3, 3]))c.unsqueeze(0), c[None, :](tensor([[10., 20., 30.]]), tensor([[10., 20., 30.]]))m[:,:, None]tensor([[[1],
[2],
[3]],
[[4],
[5],
[6]],
[[7],
[8],
[9]]])c.shape, c.unsqueeze(0).shape(torch.Size([3]), torch.Size([1, 3]))c.unsqueeze(1), c[: ,None](tensor([[10.],
[20.],
[30.]]),
tensor([[10.],
[20.],
[30.]]))c.shape, c.unsqueeze(1).shape(torch.Size([3]), torch.Size([3, 1]))c[None].shape, c[...,None].shape(torch.Size([1, 3]), torch.Size([3, 1]))c[: ,None].expand_as(m)tensor([[10., 10., 10.],
[20., 20., 20.],
[30., 30., 30.]])m + c[:, None]tensor([[11., 12., 13.],
[24., 25., 26.],
[37., 38., 39.]])m + c[None, :]tensor([[11., 22., 33.],
[14., 25., 36.],
[17., 28., 39.]])c[None, :] * c[:, None]tensor([[100., 200., 300.],
[200., 400., 600.],
[300., 600., 900.]])c[None, :] > c[:, None]tensor([[False, True, True],
[False, False, True],
[False, False, False]])ctensor([10., 20., 30.])m * mtensor([[ 1, 4, 9],
[16, 25, 36],
[49, 64, 81]])Matmul with broadcasting
digit = m1[0]
digit.shape, m2.shape(torch.Size([784]), torch.Size([784, 10]))digit[:,None].shapetorch.Size([784, 1])digit[:,None].expand_as(m2).shapetorch.Size([784, 10])(digit[:,None]* m2).shapetorch.Size([784, 10])def matmul(a, b):
(ar,ac),(br,bc) = a.shape, b.shape
t1 = torch.zeros(ar, bc)
for i in range(ar): #5
for j in range(bc): #10
# t1[i,j] = (a[i,:] * b[:, j]).sum()
# t1[i,j] = torch.dot(a[i,:], b[:, j])
t1[i] = (a[i, :, None] * b).sum(dim = 0)
return t1test_close(t1, matmul(m1, m2))1.34 ms ± 27.4 µs per loop (mean ± std. dev. of 7 runs, 50 loops each)result=matmul(m1, m2)
resulttensor([[-10.94, -0.68, -7.00, -4.01, -2.09, -3.36, 3.91, -3.44, -11.47, -2.12],
[ 14.54, 6.00, 2.89, -4.08, 6.59, -14.74, -9.28, 2.16, -15.28, -2.68],
[ 2.22, -3.22, -4.80, -6.05, 14.17, -8.98, -4.79, -5.44, -20.68, 13.57],
[ -6.71, 8.90, -7.46, -7.90, 2.70, -4.73, -11.03, -12.98, -6.44, 3.64],
[ -2.44, -6.40, -2.40, -9.04, 11.18, -5.77, -8.92, -3.79, -8.98, 5.28]])tr = matmul(x_train, weights)
tr.shape,tr(torch.Size([50000, 10]),
tensor([[ 0.96, -2.96, -2.11, ..., -15.09, -17.69, 0.60],
[ 6.89, -0.34, 0.79, ..., -17.13, -25.36, 16.23],
[-10.18, 7.38, 4.13, ..., -6.73, -6.79, -1.58],
...,
[ 7.40, 7.64, -3.50, ..., -1.02, -16.22, 2.07],
[ 3.25, 9.52, -9.37, ..., 2.98, -19.58, -1.96],
[ 15.70, 4.12, -5.62, ..., 8.08, -12.21, 0.42]]))CPU times: user 14 s, sys: 8.28 ms, total: 14 s
Wall time: 13.1 s26.3 µs ± 6.27 µs per loop (mean ± std. dev. of 7 runs, 50 loops each)50.7 ms ± 5.95 ms per loop (mean ± std. dev. of 7 runs, 5 loops each)The slowest run took 6.67 times longer than the fastest. This could mean that an intermediate result is being cached.
8.14 µs ± 8.83 µs per loop (mean ± std. dev. of 7 runs, 50 loops each)13.3 ms ± 1.75 ms per loop (mean ± std. dev. of 7 runs, 5 loops each)Einstein Summation
einsumis a compact representation for combining products and sums in a general way.
m1.shape, m2.shape(torch.Size([5, 784]), torch.Size([784, 10]))mr = torch.einsum('ik,kj->ikj',m1,m2)
mr.shapetorch.Size([5, 784, 10])mr.sum(1)tensor([[-10.94, -0.68, -7.00, -4.01, -2.09, -3.36, 3.91, -3.44, -11.47, -2.12],
[ 14.54, 6.00, 2.89, -4.08, 6.59, -14.74, -9.28, 2.16, -15.28, -2.68],
[ 2.22, -3.22, -4.80, -6.05, 14.17, -8.98, -4.79, -5.44, -20.68, 13.57],
[ -6.71, 8.90, -7.46, -7.90, 2.70, -4.73, -11.03, -12.98, -6.44, 3.64],
[ -2.44, -6.40, -2.40, -9.04, 11.18, -5.77, -8.92, -3.79, -8.98, 5.28]])mr = torch.einsum('ik,kj->ij',m1,m2)def matmul(a, b): return torch.einsum('ik,kj->ij',a,b)test_close(tr, matmul(x_train, weights), eps=1e-3)11.3 ms ± 177 µs per loop (mean ± std. dev. of 7 runs, 5 loops each)pytorch op
test_close(tr, x_train@weights, eps=1e-3)12.5 ms ± 2.99 ms per loop (mean ± std. dev. of 7 runs, 5 loops each)CUDA
!conda list | grep cudatoolkitcudatoolkit 11.8.0 h4ba93d1_12 conda-forgedef matmul(grid, a, b, c):
i, j = grid
if i < c.shape[0] and j < c.shape[1]:
tmp = 0.
for k in range(a.shape[1]):
tmp += a[i, k] * b[k, j]
c[i, j] = tmpres = torch.zeros(ar,bc)
matmul((0,0), m1, m2, res)
restensor([[-10.94, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00],
[ 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00],
[ 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00],
[ 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00],
[ 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00]])def launch_kernel(kernel, grid_x, grid_y, *args, **kwargs):
for i in range(grid_x):
for j in range(grid_y):
kernel((i, j), *args, **kwargs)res = torch.zeros(ar, bc)
launch_kernel(matmul, ar, bc, m1, m2, res)
restensor([[-10.94, -0.68, -7.00, -4.01, -2.09, -3.36, 3.91, -3.44, -11.47, -2.12],
[ 14.54, 6.00, 2.89, -4.08, 6.59, -14.74, -9.28, 2.16, -15.28, -2.68],
[ 2.22, -3.22, -4.80, -6.05, 14.17, -8.98, -4.79, -5.44, -20.68, 13.57],
[ -6.71, 8.90, -7.46, -7.90, 2.70, -4.73, -11.03, -12.98, -6.44, 3.64],
[ -2.44, -6.40, -2.40, -9.04, 11.18, -5.77, -8.92, -3.79, -8.98, 5.28]])from numba import cuda@cuda.jit
def matmul(a,b,c):
i, j = cuda.grid(2)
if i < c.shape[0] and j < c.shape[1]:
tmp = 0.
for k in range(a.shape[1]):
tmp += a[i, k] * b[k, j]
c[i, j] = tmpr = np.zeros(tr.shape)
#m1g, m2g, rg = cuda.to_device(x_train), cuda.to_device(weights), cuda.to_device(r)m1g, m2g, rg = map(cuda.to_device, (x_train, weights, r))m1g, m1g.shape(<numba.cuda.cudadrv.devicearray.DeviceNDArray>,
(50000, 784))TPB = 16
rr, rc = r.shape
blockspergrid = (math.ceil(rr / TPB), math.ceil(rc / TPB))
blockspergrid(3125, 1)matmul[blockspergrid, (TPB, TPB)](m1g, m2g, rg)r = rg.copy_to_host()
test_close(tr, r, eps=1e-3)matmul[blockspergrid, (TPB, TPB)](m1g, m2g, rg)
r = rg.copy_to_host()m1c, m2c = x_train.cuda(), weights.cuda()
m1gpu, m2gpu = m1.cuda(), m2.cuda()cpu() copys from GPU to CPU
r = (m1c @ m2c).cpu()The slowest run took 7.32 times longer than the fastest. This could mean that an intermediate result is being cached.
126 µs ± 113 µs per loop (mean ± std. dev. of 7 runs, 50 loops each)1.24 ms ± 28.4 µs per loop (mean ± std. dev. of 7 runs, 50 loops each)r, r.shape(tensor([[ 0.96, -2.96, -2.11, ..., -15.09, -17.69, 0.60],
[ 6.89, -0.34, 0.79, ..., -17.13, -25.36, 16.23],
[-10.18, 7.38, 4.13, ..., -6.73, -6.79, -1.58],
...,
[ 7.40, 7.64, -3.50, ..., -1.02, -16.22, 2.07],
[ 3.25, 9.52, -9.37, ..., 2.98, -19.58, -1.96],
[ 15.70, 4.12, -5.62, ..., 8.08, -12.21, 0.42]]),
torch.Size([50000, 10]))import gc
import torch
torch.cuda.empty_cache()
gc.collect()90import ctypes
libc = ctypes.CDLL("libc.so.6") # clearing cache
libc.malloc_trim(0)1for name in dir():
if not name.startswith('_'):
del globals()[name]Clustering
Clustering techniques are unsupervised learning algorithms that try to group unlabelled data into “clusters”, using the (typically spatial) structure of the data itself.
import math, matplotlib.pyplot as plt, operator, torch
from functools import partialtorch.manual_seed(42)
torch.set_printoptions(precision = 3, linewidth = 140, sci_mode = False)Create data
n_clusters= 6
n_samples = 250
centroids = torch.rand(n_clusters, 2) * 70 - 35
centroidstensor([[ 26.759, 29.050],
[ -8.200, 32.151],
[ -7.669, 7.063],
[-17.040, 20.555],
[ 30.854, -25.677],
[ 30.422, 6.551]])from torch.distributions.multivariate_normal import MultivariateNormal
from torch import tensordef sample(m):
return MultivariateNormal(m,
torch.diag(tensor([5.,5.]))).sample((n_samples,))slices = [sample(c) for c in centroids]
data = torch.cat(slices)
data.shapetorch.Size([1500, 2])def plot_data(centroids, data, n_samples, ax = None):
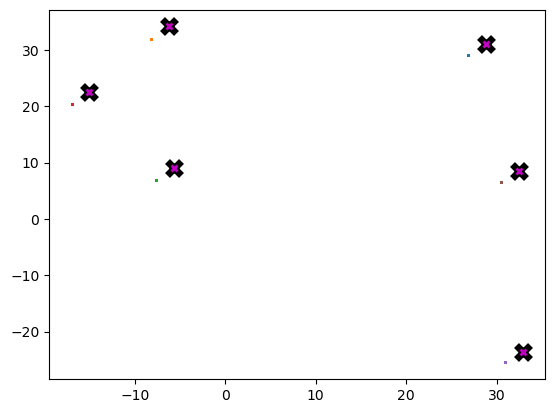
if ax is None: _,ax = plt.subplots()
for i, centroid in enumerate(centroids):
samples = data[i * n_samples:(i + 1) * n_samples]
ax.scatter(samples[:,0], samples[:,1], s = 1)
ax.plot(*centroid, markersize=10, marker = "x", color='k', mew = 5)
ax.plot(*centroid, markersize=5, marker= "x", color = 'm', mew = 2)plot_data(centroids, data, n_samples)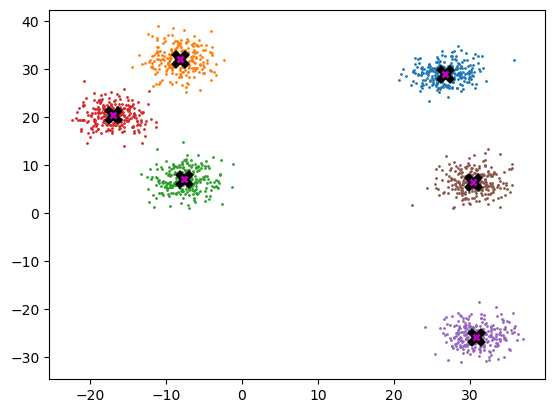
Mean shift
midp = data.mean(0)
midptensor([ 9.222, 11.604])plot_data([midp]*6, data, n_samples)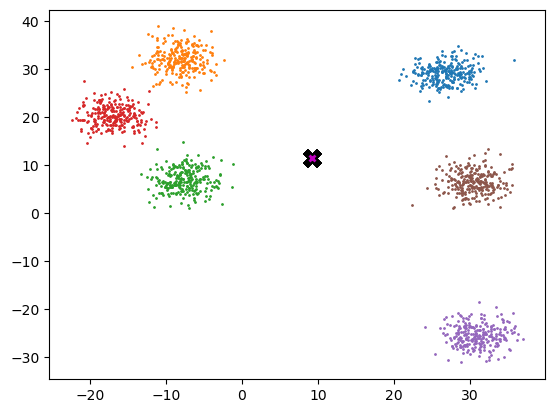
def gaussian(d, bw):
return torch.exp(-0.5*((d/bw))**2) / (bw * math.sqrt(2*math.pi))def plot_func(f):
x = torch.linspace(0, 10, 100)
plt.plot(x, f(x))plot_func(partial(gaussian, bw=2.5))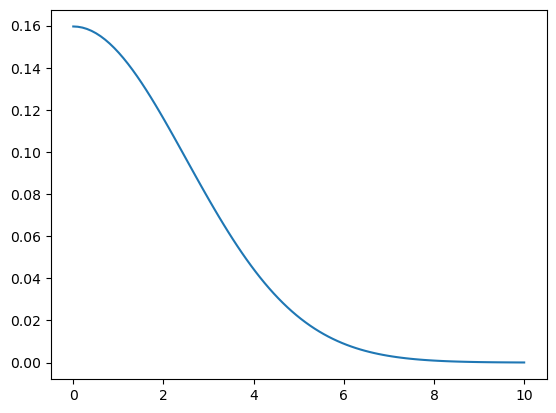
f = partial(gaussian, bw=2.5)f(tensor(4.))tensor(0.044)def tri(d, i): return (-d + i).clamp_min(0)/iplot_func(partial(tri, i = 8))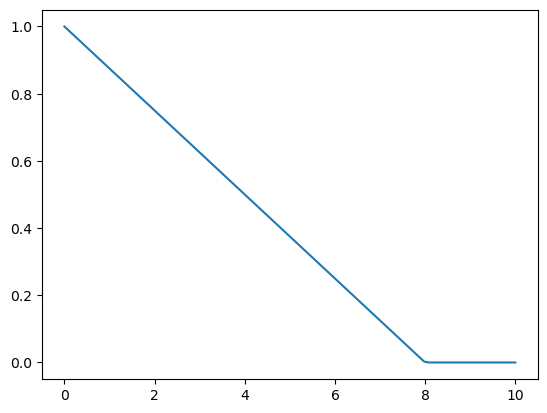
X = data.clone()
x = data[0]
xtensor([26.204, 26.349])x.shape, X.shape, x[None].shape(torch.Size([2]), torch.Size([1500, 2]), torch.Size([1, 2]))(x- X)[:8]tensor([[ 0.000, 0.000],
[ 0.513, -3.865],
[-4.227, -2.345],
[ 0.557, -3.685],
[-5.033, -3.745],
[-4.073, -0.638],
[-3.415, -5.601],
[-1.920, -5.686]])dist = torch.einsum('ik->i',((x - X) ** 2))
dist.sqrt()tensor([ 0.000, 3.899, 4.834, ..., 17.628, 22.610, 21.617])dist = ((x - X) ** 2).sum(1).sqrt()
disttensor([ 0.000, 3.899, 4.834, ..., 17.628, 22.610, 21.617])weight = gaussian(dist, 2.5)
weight[:8]tensor([0.160, 0.047, 0.025, 0.053, 0.007, 0.041, 0.005, 0.009])weight.shape,weight[:,None].shape, X.shape(torch.Size([1500]), torch.Size([1500, 1]), torch.Size([1500, 2]))weight[:,None] * Xtensor([[ 4.182, 4.205],
[ 1.215, 1.429],
[ 0.749, 0.706],
...,
[ 0.000, 0.000],
[ 0.000, 0.000],
[ 0.000, 0.000]])def one_update(X):
for i, x in enumerate(X):
dist = torch.einsum('ik->i',((x - X) ** 2))
weight = gaussian(dist, 2.5)
X[i] = (weight[:, None] * X).sum(0)/weight.sum()def meanshift(data):
X = data.clone()
for it in range(5): one_update(X)
return XCPU times: user 867 ms, sys: 144 µs, total: 867 ms
Wall time: 866 msplot_data(centroids+2, X, n_samples)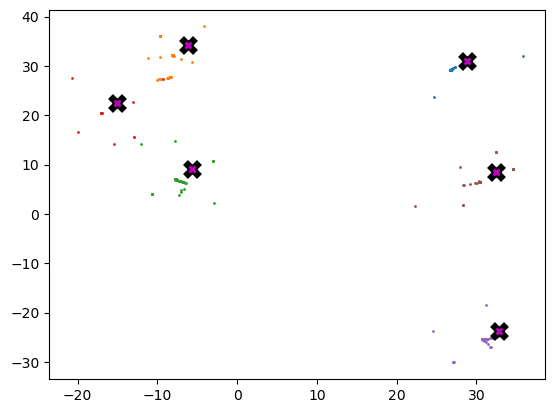
Animation
from matplotlib.animation import FuncAnimation
from IPython.display import HTMLdef do_one(d):
if d: one_update(X)
ax.clear()
plot_data(centroids+2, X, n_samples, ax = ax)X = data.clone()
fig, ax = plt.subplots()
ani = FuncAnimation(fig, do_one, frames = 5, interval=500, repeat=False)
plt.close()
HTML(ani.to_jshtml())GPU batched algorithm
bs = 5
X = data.clone()
x = X[:bs]
x.shape, X.shape(torch.Size([5, 2]), torch.Size([1500, 2]))def dist_b(a, b):
return (((a[None] -b[:,None])**2).sum(2)).sqrt()dist_b(X,x)tensor([[ 0.000, 3.899, 4.834, ..., 17.628, 22.610, 21.617],
[ 3.899, 0.000, 4.978, ..., 21.499, 26.508, 25.500],
[ 4.834, 4.978, 0.000, ..., 19.373, 24.757, 23.396],
[ 3.726, 0.185, 4.969, ..., 21.335, 26.336, 25.333],
[ 6.273, 5.547, 1.615, ..., 20.775, 26.201, 24.785]])dist_b(X,x).shapetorch.Size([5, 1500])X[None,:].shape, x[:,None].shape, (X[None, :] - x[:, None]).shape(torch.Size([1, 1500, 2]), torch.Size([5, 1, 2]), torch.Size([5, 1500, 2]))gaussian??Signature: gaussian(d, bw) Docstring: <no docstring> Source: def gaussian(d, bw): return torch.exp(-0.5*((d/bw))**2) / (bw * math.sqrt(2*math.pi)) File: /tmp/ipykernel_1054164/117635507.py Type: function
weight = gaussian(dist_b(X,x),2)weight.shape, X.shape(torch.Size([5, 1500]), torch.Size([1500, 2]))weight[..., None].shape, x[None].shape(torch.Size([5, 1500, 1]), torch.Size([1, 5, 2]))num = (weight[...,None] * X[None]).sum(1)
num.shapetorch.Size([5, 2])numtensor([[367.870, 386.231],
[518.332, 588.680],
[329.665, 330.782],
[527.617, 598.217],
[231.302, 234.155]])torch.einsum('ij,jk ->ik', weight, X)tensor([[367.870, 386.231],
[518.332, 588.680],
[329.665, 330.782],
[527.617, 598.217],
[231.302, 234.155]])weight@Xtensor([[367.870, 386.231],
[518.332, 588.680],
[329.665, 330.782],
[527.617, 598.217],
[231.302, 234.155]])div = weight.sum(1, keepdim = True)
div.shapetorch.Size([5, 1])num/divtensor([[26.376, 27.692],
[26.101, 29.643],
[28.892, 28.990],
[26.071, 29.559],
[29.323, 29.685]])bs = 5def meanshift(data, bs = 500):
n = len(data)
X = data.clone()
for it in range(5):
for i in range(0, n, bs):
s = slice(i, min(i+bs, n))
weight = gaussian(dist_b(X, X[s]), 2.5)
div = weight.sum(1, keepdim = True)
X[s] = weight@X/div
return Xdata = data.cuda()X = meanshift(data,bs).cpu()17.7 ms ± 1.79 ms per loop (mean ± std. dev. of 7 runs, 5 loops each)3.91 ms ± 11.2 µs per loop (mean ± std. dev. of 7 runs, 5 loops each)3.68 ms ± 8.66 µs per loop (mean ± std. dev. of 7 runs, 5 loops each)plot_data(centroids+2, X, n_samples)