Principal Component Analysis

For Dimensionality reduction technique 
from sklearn.datasets import load_digits
import pandas as pd

dataset = load_digits()
dataset.keys()
dict_keys(['data', 'target', 'frame', 'feature_names', 'target_names', 'images', 'DESCR'])
dataset.data.shape
(1797, 64)
dataset.data[0]
array([ 0.,  0.,  5., 13.,  9.,  1.,  0.,  0.,  0.,  0., 13., 15., 10.,
       15.,  5.,  0.,  0.,  3., 15.,  2.,  0., 11.,  8.,  0.,  0.,  4.,
       12.,  0.,  0.,  8.,  8.,  0.,  0.,  5.,  8.,  0.,  0.,  9.,  8.,
        0.,  0.,  4., 11.,  0.,  1., 12.,  7.,  0.,  0.,  2., 14.,  5.,
       10., 12.,  0.,  0.,  0.,  0.,  6., 13., 10.,  0.,  0.,  0.])
dataset.data[0].reshape(8,8)
array([[ 0.,  0.,  5., 13.,  9.,  1.,  0.,  0.],
       [ 0.,  0., 13., 15., 10., 15.,  5.,  0.],
       [ 0.,  3., 15.,  2.,  0., 11.,  8.,  0.],
       [ 0.,  4., 12.,  0.,  0.,  8.,  8.,  0.],
       [ 0.,  5.,  8.,  0.,  0.,  9.,  8.,  0.],
       [ 0.,  4., 11.,  0.,  1., 12.,  7.,  0.],
       [ 0.,  2., 14.,  5., 10., 12.,  0.,  0.],
       [ 0.,  0.,  6., 13., 10.,  0.,  0.,  0.]])
from matplotlib import pyplot as plt

plt.gray()
plt.matshow(dataset.data[0].reshape(8,8))
<Figure size 640x480 with 0 Axes>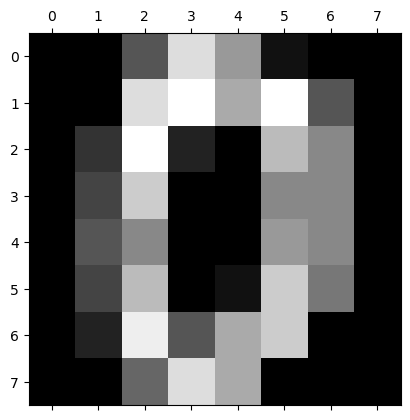

plt.matshow(dataset.data[9].reshape(8,8))

dataset.target[:5]
array([0, 1, 2, 3, 4])
df = pd.DataFrame(dataset.data, columns=dataset.feature_names)
df.head()
pixel_0_0 pixel_0_1 pixel_0_2 pixel_0_3 pixel_0_4 pixel_0_5 pixel_0_6 pixel_0_7 pixel_1_0 pixel_1_1 ... pixel_6_6 pixel_6_7 pixel_7_0 pixel_7_1 pixel_7_2 pixel_7_3 pixel_7_4 pixel_7_5 pixel_7_6 pixel_7_7
0 0.0 0.0 5.0 13.0 9.0 1.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 6.0 13.0 10.0 0.0 0.0 0.0
1 0.0 0.0 0.0 12.0 13.0 5.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 11.0 16.0 10.0 0.0 0.0
2 0.0 0.0 0.0 4.0 15.0 12.0 0.0 0.0 0.0 0.0 ... 5.0 0.0 0.0 0.0 0.0 3.0 11.0 16.0 9.0 0.0
3 0.0 0.0 7.0 15.0 13.0 1.0 0.0 0.0 0.0 8.0 ... 9.0 0.0 0.0 0.0 7.0 13.0 13.0 9.0 0.0 0.0
4 0.0 0.0 0.0 1.0 11.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 2.0 16.0 4.0 0.0 0.0

5 rows × 64 columns

dataset.target
array([0, 1, 2, ..., 8, 9, 8])
df.describe()
pixel_0_0 pixel_0_1 pixel_0_2 pixel_0_3 pixel_0_4 pixel_0_5 pixel_0_6 pixel_0_7 pixel_1_0 pixel_1_1 ... pixel_6_6 pixel_6_7 pixel_7_0 pixel_7_1 pixel_7_2 pixel_7_3 pixel_7_4 pixel_7_5 pixel_7_6 pixel_7_7
count 1797.0 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000 ... 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000 1797.000000
mean 0.0 0.303840 5.204786 11.835838 11.848080 5.781859 1.362270 0.129661 0.005565 1.993879 ... 3.725097 0.206455 0.000556 0.279354 5.557596 12.089037 11.809126 6.764051 2.067891 0.364496
std 0.0 0.907192 4.754826 4.248842 4.287388 5.666418 3.325775 1.037383 0.094222 3.196160 ... 4.919406 0.984401 0.023590 0.934302 5.103019 4.374694 4.933947 5.900623 4.090548 1.860122
min 0.0 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 ... 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
25% 0.0 0.000000 1.000000 10.000000 10.000000 0.000000 0.000000 0.000000 0.000000 0.000000 ... 0.000000 0.000000 0.000000 0.000000 1.000000 11.000000 10.000000 0.000000 0.000000 0.000000
50% 0.0 0.000000 4.000000 13.000000 13.000000 4.000000 0.000000 0.000000 0.000000 0.000000 ... 1.000000 0.000000 0.000000 0.000000 4.000000 13.000000 14.000000 6.000000 0.000000 0.000000
75% 0.0 0.000000 9.000000 15.000000 15.000000 11.000000 0.000000 0.000000 0.000000 3.000000 ... 7.000000 0.000000 0.000000 0.000000 10.000000 16.000000 16.000000 12.000000 2.000000 0.000000
max 0.0 8.000000 16.000000 16.000000 16.000000 16.000000 16.000000 15.000000 2.000000 16.000000 ... 16.000000 13.000000 1.000000 9.000000 16.000000 16.000000 16.000000 16.000000 16.000000 16.000000

8 rows × 64 columns

X = df
y = dataset.target
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_scaled
array([[ 0.        , -0.33501649, -0.04308102, ..., -1.14664746,
        -0.5056698 , -0.19600752],
       [ 0.        , -0.33501649, -1.09493684, ...,  0.54856067,
        -0.5056698 , -0.19600752],
       [ 0.        , -0.33501649, -1.09493684, ...,  1.56568555,
         1.6951369 , -0.19600752],
       ...,
       [ 0.        , -0.33501649, -0.88456568, ..., -0.12952258,
        -0.5056698 , -0.19600752],
       [ 0.        , -0.33501649, -0.67419451, ...,  0.8876023 ,
        -0.5056698 , -0.19600752],
       [ 0.        , -0.33501649,  1.00877481, ...,  0.8876023 ,
        -0.26113572, -0.19600752]])
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=30)
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
model.score(X_test, y_test)
0.9722222222222222

Use PCA to reduce dimensions 

X
pixel_0_0 pixel_0_1 pixel_0_2 pixel_0_3 pixel_0_4 pixel_0_5 pixel_0_6 pixel_0_7 pixel_1_0 pixel_1_1 ... pixel_6_6 pixel_6_7 pixel_7_0 pixel_7_1 pixel_7_2 pixel_7_3 pixel_7_4 pixel_7_5 pixel_7_6 pixel_7_7
0 0.0 0.0 5.0 13.0 9.0 1.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 6.0 13.0 10.0 0.0 0.0 0.0
1 0.0 0.0 0.0 12.0 13.0 5.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 11.0 16.0 10.0 0.0 0.0
2 0.0 0.0 0.0 4.0 15.0 12.0 0.0 0.0 0.0 0.0 ... 5.0 0.0 0.0 0.0 0.0 3.0 11.0 16.0 9.0 0.0
3 0.0 0.0 7.0 15.0 13.0 1.0 0.0 0.0 0.0 8.0 ... 9.0 0.0 0.0 0.0 7.0 13.0 13.0 9.0 0.0 0.0
4 0.0 0.0 0.0 1.0 11.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 2.0 16.0 4.0 0.0 0.0
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1792 0.0 0.0 4.0 10.0 13.0 6.0 0.0 0.0 0.0 1.0 ... 4.0 0.0 0.0 0.0 2.0 14.0 15.0 9.0 0.0 0.0
1793 0.0 0.0 6.0 16.0 13.0 11.0 1.0 0.0 0.0 0.0 ... 1.0 0.0 0.0 0.0 6.0 16.0 14.0 6.0 0.0 0.0
1794 0.0 0.0 1.0 11.0 15.0 1.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 2.0 9.0 13.0 6.0 0.0 0.0
1795 0.0 0.0 2.0 10.0 7.0 0.0 0.0 0.0 0.0 0.0 ... 2.0 0.0 0.0 0.0 5.0 12.0 16.0 12.0 0.0 0.0
1796 0.0 0.0 10.0 14.0 8.0 1.0 0.0 0.0 0.0 2.0 ... 8.0 0.0 0.0 1.0 8.0 12.0 14.0 12.0 1.0 0.0

1797 rows × 64 columns

Use components such that 95% of variance is retained 

from sklearn.decomposition import PCA

pca = PCA(0.95)
X_pca = pca.fit_transform(X)
X_pca.shape
(1797, 29)
pca.explained_variance_ratio_
array([0.14890594, 0.13618771, 0.11794594, 0.08409979, 0.05782415,
       0.0491691 , 0.04315987, 0.03661373, 0.03353248, 0.03078806,
       0.02372341, 0.02272697, 0.01821863, 0.01773855, 0.01467101,
       0.01409716, 0.01318589, 0.01248138, 0.01017718, 0.00905617,
       0.00889538, 0.00797123, 0.00767493, 0.00722904, 0.00695889,
       0.00596081, 0.00575615, 0.00515158, 0.0048954 ])
pca.n_components_
29

PCA created 29 components out of 64 original columns

X_pca
array([[ -1.25946645,  21.27488348,  -9.46305462, ...,   3.67072108,
         -0.9436689 ,  -1.13250195],
       [  7.9576113 , -20.76869896,   4.43950604, ...,   2.18261819,
         -0.51022719,   2.31354911],
       [  6.99192297,  -9.95598641,   2.95855808, ...,   4.22882114,
          2.1576573 ,   0.8379578 ],
       ...,
       [ 10.8012837 ,  -6.96025223,   5.59955453, ...,  -3.56866194,
          1.82444444,   3.53885886],
       [ -4.87210009,  12.42395362, -10.17086635, ...,   3.25330054,
          0.95484174,  -0.93895602],
       [ -0.34438963,   6.36554919,  10.77370849, ...,  -3.01636722,
          1.29752723,   2.58810313]])
X_train_pca, X_test_pca, y_train, y_test = train_test_split(X_pca, y, test_size=0.2, random_state=30)
from sklearn.linear_model import LogisticRegression

model = LogisticRegression(max_iter=1000)
model.fit(X_train_pca, y_train)
model.score(X_test_pca, y_test)
0.9694444444444444

Let’s now select only two components

pca = PCA(n_components=16)
X_pca = pca.fit_transform(X)
X_pca.shape
(1797, 16)
X_pca
array([[ -1.2594598 ,  21.27487967,  -9.46303989, ...,  -3.31223438,
          6.02583852,   2.68741732],
       [  7.95761297, -20.7686941 ,   4.43950445, ...,  -6.50507014,
         -2.27310577,  -2.14622234],
       [  6.99193119,  -9.95600512,   2.95858793, ...,   6.83484372,
         -1.65925951,  -4.25884236],
       ...,
       [ 10.80128998,  -6.96027365,   5.5995876 , ...,   1.24767177,
          2.62633682,  -5.79460334],
       [ -4.87210168,  12.42396132, -10.17087749, ...,  -1.21624842,
         10.77743555,   2.38010911],
       [ -0.34438951,   6.36554076,  10.77371718, ...,   7.0540168 ,
          0.72142473,   0.27006973]])
pca.explained_variance_ratio_
array([0.14890594, 0.13618771, 0.11794594, 0.08409979, 0.05782415,
       0.0491691 , 0.04315987, 0.03661373, 0.03353248, 0.03078806,
       0.02372336, 0.02272696, 0.01821856, 0.01773823, 0.01466903,
       0.01409675])

You can see that both combined retains 0.14+0.13=0.27 or 27% of important feature information

X_train_pca, X_test_pca, y_train, y_test = train_test_split(X_pca, y, test_size=0.2, random_state=30)

model = LogisticRegression(max_iter=1000)
model.fit(X_train_pca, y_train)
model.score(X_test_pca, y_test)
0.9472222222222222

We get less accuancy (~60%) as using only 2 components did not retain much of the feature information. However in real life you will find many cases where using 2 or few PCA components can still give you a pretty good accuracy

Back to top